PLINK pca
#coding:utf-8
__author__ = 'similarface'
import os
import pandas as pd
import matplotlib.pyplot as plt path='plink.eigenvec' def plinkPca(filepath,header=""):
data=pd.read_table(path,header=None,sep=' ')
filterdata=data.loc[:,0:5]
label=filterdata[0].tolist()
label_uniq = list(set(label))
label_uniq.sort(key=label.index)
filterdata.columns=['pop','human','pca0','pca1','pca2','pca3']
colors=['gold', 'red', 'blue', 'green', 'black', 'yellow', 'orangered', 'sienna', 'tomato', 'silver', 'fuchsia', 'orange', 'coral', 'orchid', 'magenta', 'chartreuse', 'navy', 'violet', 'beige', 'khaki', 'tan', 'indigo', 'cyan', 'azure', 'teal']
colors=colors[0:len(label_uniq)]
markers = ['o', 'x', 's', 'p', '^', '>', '+', 'D', '*', '<', '','_']*10
markers=markers[0:len(label_uniq)]
#调整画布大小
fig = plt.figure(figsize=(8,8),dpi=100)
plt.clf()
for i,targer_name,color,marker in zip(range(len(label_uniq)),label_uniq,colors,markers):
plt.scatter(filterdata[filterdata['pop']==targer_name]['pca0'],filterdata[filterdata['pop']==targer_name]['pca1'], s=20, edgecolor='k',c=color,marker=marker)
plt.legend(labels = label_uniq, bbox_to_anchor=(1.0,0.95))
plt.title(header)
plt.show() plinkPca(path,header="EUR PCA")
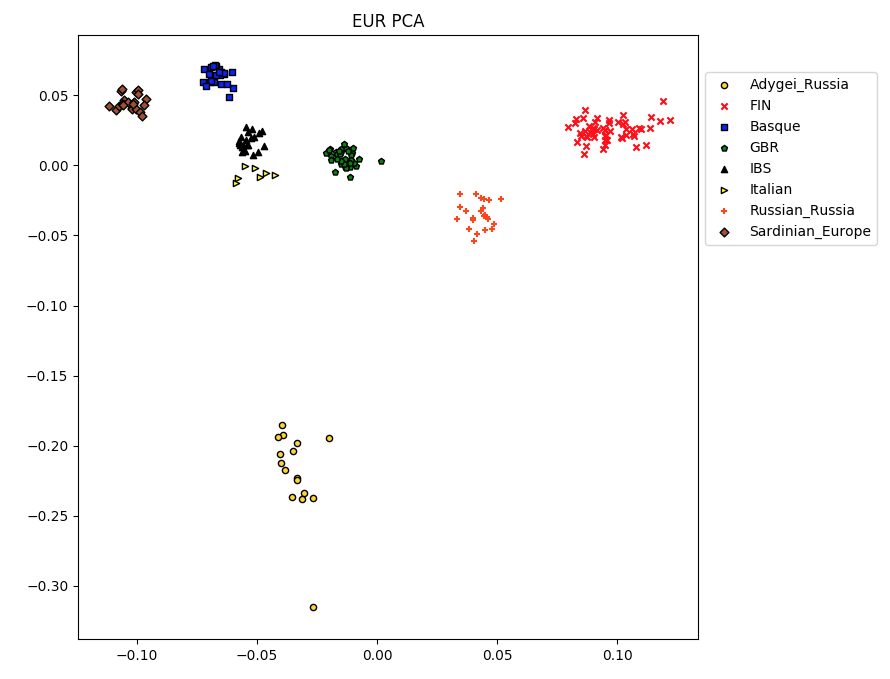
PLINK pca的更多相关文章
- GWAS群体分层 (Population stratification):利用plink对基因型进行PCA
一.为什么要做祖先成分的PCA? GWAS研究时经常碰到群体分层的现象,即该群体的祖先来源多样性,我们知道的,不同群体SNP频率不一样,导致后面做关联分析的时候可能出现假阳性位点(不一定是显著信号位点 ...
- plink 进行PCA分析
当我们进行群体遗传分析时,得到vcf后,可利用plink进行主成分(PCA)分析: 一.软件安装 1 conda install plink 二.使用流程 第一步:将vcf转换为plink格式 1 p ...
- EIGENSTRAT计算PCA的显著性
之前我写过一篇文章群体遗传分析分层校正,该选用多少个PCA?,里面提到可以通过EIGENSTRAT软件确定显著的主成分,后续就可以将显著的主成分加入协变量中. 这篇文章主要是讲如何通过EIGENSTR ...
- Eigensoft-smartpca分析PCA报错:warning (mapfile): bad chrom: Segmentation fault
目录 问题 解决 问题 一直以来用Eigensoft的smartpca来做群体遗传的PCA分析很顺畅,结果也比较靠谱. 但今天报错如下: $ ~/miniconda3/bin/smartpca -p ...
- 用scikit-learn学习主成分分析(PCA)
在主成分分析(PCA)原理总结中,我们对主成分分析(以下简称PCA)的原理做了总结,下面我们就总结下如何使用scikit-learn工具来进行PCA降维. 1. scikit-learn PCA类介绍 ...
- 主成分分析(PCA)原理总结
主成分分析(Principal components analysis,以下简称PCA)是最重要的降维方法之一.在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用.一般我们提到降维最容易想到的算法就 ...
- 机器学习基础与实践(三)----数据降维之PCA
写在前面:本来这篇应该是上周四更新,但是上周四写了一篇深度学习的反向传播法的过程,就推迟更新了.本来想参考PRML来写,但是发现里面涉及到比较多的数学知识,写出来可能不好理解,我决定还是用最通俗的方法 ...
- 数据降维技术(1)—PCA的数据原理
PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降 ...
- 深度学习笔记——PCA原理与数学推倒详解
PCA目的:这里举个例子,如果假设我有m个点,{x(1),...,x(m)},那么我要将它们存在我的内存中,或者要对着m个点进行一次机器学习,但是这m个点的维度太大了,如果要进行机器学习的话参数太多, ...
随机推荐
- 关于Java设计模式的一些概况
设计模式(Design pattern)在软件行业一直都扮演着很重要的角色.最近感觉自己对设计模式的知识有些遗忘了,虽然以前也看了很多,但是坦白说,其实并没有怎么理解.基本还是为了应付面试.然后,在工 ...
- python3 str和bytes之间转换
a bytes-like object is required, not 'str' 碰到 这个错误 ,是因为需要是的bytes,不是str bytes -> str: 1 str-> ...
- linux面试题目—2
linux面试题目—2 二 选择题 1.关闭linux系统(不重新启动)可使用命令 B . A Ctrl+Alt+Del B halt C shutdown -r now D reboot 2.实现从 ...
- lumisoft会将eml后缀格式的附件给解析成文本,这里保存成文件
MIME_Entity[] attachments = mime.Attachments; foreach (MIME_Entity entity in attachments) { string f ...
- 数据库建模软件ERStudio-表关系建模详解
ERStudio是优秀的数据库建模软件,它不仅可以建立表.视图等模型,还可以建立多表间各种关系的模型,另外还可以根据模型生成表到数据库,下面具体讲解一下它的表关系建模. 1. 首先讲一下怎么建立表关系 ...
- scrapy-splash抓取动态数据例子三
一.介绍 本例子用scrapy-splash抓取今日头条网站给定关键字抓取咨询信息. 给定关键字:打通:融合:电视 抓取信息内如下: 1.资讯标题 2.资讯链接 3.资讯时间 4.资讯来源 二.网站信 ...
- 通过web php 执行shell脚本,获取的结果与直接在命令行下获取的结果不同。
公司项目中的一项小功能,统计设备的连接数.其中用到shell脚本来获取已连接设备的统计.使用命令 /bin/netstat -an| grep ESTABLISHED | awk '{print $4 ...
- Mach-O文件格式和程序从载入到运行过程
> 之前深入了解过.过去了一年多的时间.如今花些时间好好总结下,毕竟好记性不如烂笔头. 其次另一个目的,对于mach-o文件结构.关于动态载入信息那个数据区中,命令含义没有深刻掰扯清除,希望有同 ...
- gensim自然语言处理(续)
上一篇,已经实现了如何将一条语句在一个语料库中比较相似度, 发现运行的时候每次都要编译语料库,通过查找资料,可以一次性编译成预料库,存人文件 编译语料库代码 11_k.py import sysimp ...
- vue 仿ele 开发流程
技术栈: vue2 vuex vue-router axios webpack eslint better-scroll 1.安装插件 npm install vue-resource babel-r ...
