树（Tree）解题总结

定义

树是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由 n(n>0) 个有限节点组成一个具有层次关系的集合。。

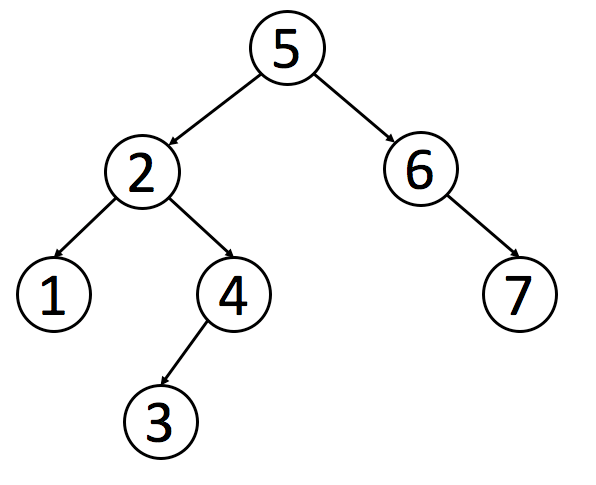
二叉搜索树（Binary Search Tree，简称 BST）是一种很常用的的二叉树。它的定义是：一个二叉树中，任意节点的值要大于等于左子树所有节点的值，且要小于等于右边子树的所有节点的值。

如下就是一个符合定义的 BST：

算法模板

void traverse(TreeNode root) {
    // root 需要做什么？在这做。
    // 其他的不用 root 操心，抛给框架
    traverse(root.left);
    traverse(root.right);
}

在二叉树框架之上，扩展出一套 BST 遍历框架：

void BST(TreeNode root, int target) {
    if (root.val == target)
        // 找到目标，做点什么
    if (root.val < target)
        BST(root.right, target);
    if (root.val > target)
        BST(root.left, target);
}

前序遍历（递归）：

List<int> preorder(TreeNode root) {
     List<int> ans = new List<int>();
     if (root == null) {
         return ans;
     }

     ans.Add(root.Val);
     ans.AddRange(preorder(root.Left));
     ans.AddRange(preorder(root.Right));
     return ans;
}

中序遍历（递归）：

List<int> inorder(TreeNode root) {
     List<int> ans = new List<int>();
     if (root == null) {
         return ans;
     }

     ans.AddRange(preorder(root.Left));
     ans.Add(root.Val);
     ans.AddRange(preorder(root.Right));
     return ans;
}

后序遍历（递归）：

List<int> postorder(TreeNode root) {
     List<int> ans = new List<int>();
     if (root == null) {
         return ans;
     }

     ans.AddRange(preorder(root.Left));
     ans.AddRange(preorder(root.Right));
     ans.Add(root.Val);
     return ans;
}

前序遍历（迭代/栈）：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;  //保存结果
        stack<TreeNode*> call;  //调用栈
        if(root!=nullptr) call.push(root);  //首先介入root节点
        while(!call.empty()){
            TreeNode *t = call.top();
            call.pop();  //访问过的节点弹出
            if(t!=nullptr){
                if(t->right) call.push(t->right);  //右节点先压栈，最后处理
                if(t->left) call.push(t->left);
                call.push(t);  //当前节点重新压栈（留着以后处理），因为先序遍历所以最后压栈
                call.push(nullptr);  //在当前节点之前加入一个空节点表示已经访问过了
            }else{  //空节点表示之前已经访问过了，现在需要处理除了递归之外的内容
                res.push_back(call.top()->val);  //call.top()是nullptr之前压栈的一个节点，也就是上面call.push(t)中的那个t
                call.pop();  //处理完了，第二次弹出节点（彻底从栈中移除）
            }
        }
        return res;
    }
};

中序遍历（迭代/栈）：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> call;
        if(root!=nullptr) call.push(root);
        while(!call.empty()){
            TreeNode *t = call.top();
            call.pop();
            if(t!=nullptr){
                if(t->right) call.push(t->right);
                call.push(t);  //在左节点之前重新插入该节点，以便在左节点之后处理（访问值）
                call.push(nullptr); //nullptr跟随t插入，标识已经访问过，还没有被处理
                if(t->left) call.push(t->left);
            }else{
                res.push_back(call.top()->val);
                call.pop();
            }
        }
        return res;
    }
};

后序遍历（迭代/栈）：

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> call;
        if(root!=nullptr) call.push(root);
        while(!call.empty()){
            TreeNode *t = call.top();
            call.pop();
            if(t!=nullptr){
                call.push(t);  //在右节点之前重新插入该节点，以便在最后处理（访问值）
                call.push(nullptr); //nullptr跟随t插入，标识已经访问过，还没有被处理
                if(t->right) call.push(t->right);
                if(t->left) call.push(t->left);
            }else{
                res.push_back(call.top()->val);
                call.pop();
            }
        }
        return res;
    }
};

要点

• 二叉树算法设计的总路线：把当前节点要做的事做好，其他的交给递归框架，不用当前节点操心。
• 如果当前节点会对下面的子节点有整体影响，可以通过辅助函数增长参数列表，借助参数传递信息。
• 删除二叉搜索树的节点有三种情况：
  1. A 恰好是末端节点，两个子节点都为空，那么它可以当场去世了
  2. A 只有一个非空子节点，那么它要让这个孩子接替自己的位置。
  3. A 有两个子节点，麻烦了，为了不破坏 BST 的性质，A 必须找到左子树中最大的那个节点，或者右子树中最小的那个节点来接替自己。

实战题目

1.树的遍历

• 94. 二叉树的中序遍历
• 144. 二叉树的前序遍历
• 145.二叉树的后序遍历
• 590. N叉树的后序遍历
• 589. N叉树的前序遍历
• 429. N叉树的层序遍历

2.树的操作

• 100. 相同的树
• 450. 删除二叉搜索树中的节点
• 701. 二叉搜索树中的插入操作
• 700. 二叉搜索树中的搜索
• 98. 验证二叉搜索树

参考资料

• 写树算法的套路框架
• 完全模仿递归，不变一行。秒杀全场，一劳永逸