图的DFS和BFS(邻接表)
用C++实现图的DFS和BFS(邻接表)
概述
图的储存方式有邻接矩阵和邻接表储存两种。由于邻接表的实现需要用到抽象数据结构里的链表,故稍微麻烦一些。C++自带的STL可以方便的实现List,使算法的实现变得简单起来
算法概述
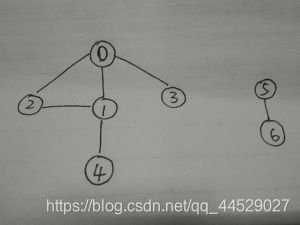
为了让我们的算法更有普适性,我们将非连通图也考虑在内。其实,要想遍历到类似于图中5,6节点这种孤岛节点,只需要依次按编号遍历顺序所有节点,如果某节点没有访问(book数组标记值为0),则从该节点开始深度优先搜索或广度优先搜索;等一次深搜或广搜完毕后,继续依次按照编号顺序遍历节点,选择从一个没访问过的结点开始再次深搜或广搜。。。如此知道把所有节点都遍历完。
代码
1.图抽象数据类型的声明,除了构造函数和析构函数之外,提供3个对外接口,分别实现递归DFS,BFS和非递归DFS(用STL栈实现)
using namespace std;
struct Graph{
//储存节点的邻接表
vector<list<int>> vertex;
//标记数组
bool book[100];
//n代表总节点个数
Graph(int n);
~Graph();
//对外接口,算法的驱动函数
void DFS_recursion_boost();
void BFS_boost();
void DFS_stack_boost();
private://内部算法实现
void DFS_recursion(int cur);
void BFS(int cur);
void DFS_stack(int cur);
};
2.图的构造函数和析构函数实现
Graph::Graph(int n){
vertex.resize(n);
for(int i=0;i<n;++i){
int adj;
cout<<"请输入"<<i<<"号节点邻接链表(以-1表示结束输入)"<<endl;
cin>>adj;
while(adj!=-1){
vertex[i].push_back(adj);
cin>>adj;
}
}
memset(book,0,sizeof(book));
}
Graph::~Graph(){
vertex.clear();
}
3.图的递归DFS调用接口及其实现函数
void Graph::DFS_recursion_boost(){
for(int i=0;i<vertex.size();++i){
DFS_recursion(i);
}
}
void Graph::DFS_recursion(int cur){
if(book[cur]==1) return;
book[cur]=1;
cout<<cur;
for(auto iter=vertex[cur].begin();iter!=vertex[cur].end();++iter){
if(book[*iter]==0){
DFS_recursion(*iter);
}
}
}
4.图的BFS调用接口及其实现函数
void Graph::BFS_boost(){
for(int i=0;i<vertex.size();++i){
BFS(i);
}
}
void Graph::BFS(int cur){
queue<int> q;
if(book[cur]==0){
q.push(cur);
}
while(!q.empty()){
int front=q.front();
q.pop();
cout<<front;
book[front]=1;
for(auto iter=vertex[front].begin();iter!=vertex[front].end();++iter){
if(book[*iter]==0){
q.push(*iter);
}
}
}
}
5.图的非递归DFS及其实现函数
void Graph::DFS_stack_boost(){
for(int i=0;i<vertex.size();++i){
DFS_stack(i);
}
}
void Graph::DFS_stack(int cur)
{
stack<int> s;
if(book[cur]==0){
s.push(cur);
}
while(!s.empty()){
int top=s.top();
if(book[top]==0){
book[top]=1;
cout<<top;
}
else{
s.pop();
// top=s.top();为何不要?
}
for(auto iter=vertex[top].begin();iter!=vertex[top].end();++iter){
if(book[*iter]==0){
s.push(*iter);
break;
}
}
}
}
6.主函数测试(注意,每次遍历后要把标记数组初始化为0)
int main(){
Graph G(7);
cout<<"递归DFS:"<<endl;
G.DFS_recursion_boost();
memset(G.book,0,100);
cout<<endl;
cout<<"BFS:"<<endl;
G.BFS_boost();
memset(G.book,0,100);
cout<<endl;
cout<<"非递归BFS:"<<endl;
G.DFS_stack_boost();
memset(G.book,0,100);
cout<<endl;
system("pause");
return 0;
}
输出
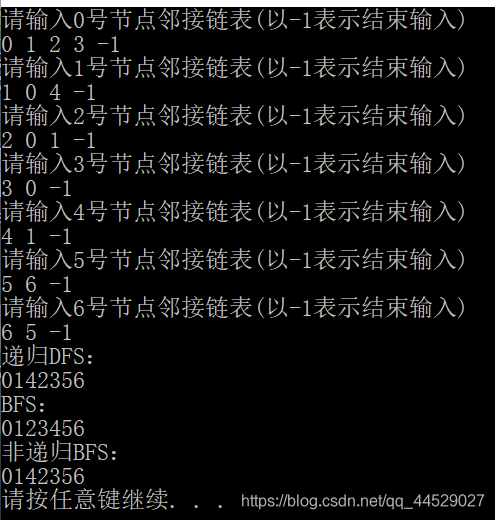
图的DFS和BFS(邻接表)的更多相关文章
- 数据结构(11) -- 邻接表存储图的DFS和BFS
/////////////////////////////////////////////////////////////// //图的邻接表表示法以及DFS和BFS //////////////// ...
- 图的DFS与BFS
图的DFS与BFS(C++) 概述 大一学生,作为我的第一篇Blog,准备记录一下图的基本操作:图的创建与遍历.请大佬多多包涵勿喷. 图可以采用邻接表,邻接矩阵,十字链表等多种储存结构进行储存,这里为 ...
- Java数据结构——图的DFS和BFS
1.图的DFS: 即Breadth First Search,深度优先搜索是从起始顶点开始,递归访问其所有邻近节点,比如A节点是其第一个邻近节点,而B节点又是A的一个邻近节点,则DFS访问A节点后再访 ...
- 【数据结构】【图文】【oj习题】 图的拓扑排序(邻接表)
拓扑排序: 按照有向图给出的次序关系,将图中顶点排成一个线性序列,对于有向图中没有限定次序关系的顶点,则可以人为加上任意的次序关系,由此所得顶点的线性序列称之为拓扑有序序列.显然对于有回路的有向图得不 ...
- 图的基本操作(基于邻接表):图的构造,深搜(DFS),广搜(BFS)
#include <iostream> #include <string> #include <queue> using namespace std; //表结点 ...
- [数据结构]图的DFS和BFS的两种实现方式
深度优先搜索 深度优先搜索,我们以无向图为例. 图的深度优先搜索(Depth First Search),和树的先序遍历比较类似. 它的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发, ...
- 图的DFS与BFS遍历
一.图的基本概念 1.邻接点:对于无向图无v1 与v2之间有一条弧,则称v1与v2互为邻接点:对于有向图而言<v1,v2>代表有一条从v1到v2的弧,则称v2为v1的邻接点. 2.度:就是 ...
- bfs 邻接表(需要优化 可能会RE *【模板】)
//---基于邻接表的bfs #include <stdio.h> #include <string.h> #include <iostream> #include ...
- hdu 4707 Pet(DFS && 邻接表)
Pet Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submis ...
随机推荐
- “git pull” 强制覆盖本地文件
放弃本地修改,使用服务器代码覆盖本地的Git命令如下: $ git fetch --all $ git reset --hard origin/master $ git pull 使用master分支 ...
- javascript算法 最短路径问题
var obj = { 1: [2, 3], 2: [1, 4, 5], 3: [1, 7, 8], 4: [2, 7], 7: [4, 8], } var 起点 = 1 var 终点 = 8 var ...
- @RequestMapping中的produces的作用和使用方式
转发:原博客 1.他的作用是指定返回值类型和返回值编码 2.consumes: 指定处理请求的提交内容类型(Content-Type),例如application/json, text/html; 一 ...
- 设计模式:visitor模式
核心:将数据结构和数据的处理分开 注意:注意函数的参数传递和调用关系 例子: class Element; class Visitor { public: virtual void Visit(Ele ...
- Monster Audio 使用教程(一)入门教程 + 常见问题
Monster Audio支持的操作系统: windows 7 64bit 至 windows 10 64bit 受支持的VST: Vst 64bit.Vst3 64bit 受支持的声卡驱动: ASI ...
- PHPSTORM断点调试配置
一.安装Xdebug xdebug官方提供了一个非常友好的安装指导: https://xdebug.org/wizard.php 打开上面的网站,将你的phpinfo页面输出的内容复制到表单中,然后点 ...
- 如何系统地学习Excel?
人在江湖,生不由己.人在职场,Excel必备. 为了帮助更多人快速掌握职场必备技能Excel,我写了一个免费的教程<职场Excel>,能帮助你解决99%职场中遇到的问题. 对,你没看错,是 ...
- 重置spyder 解决 gbk 编码不能读取问题
重置spyder 解决 gbk 编码不能读取问题 2020-06-18
- java反序列化——apache-shiro复现分析
本文首发于“合天智汇”公众号 作者:Fortheone 看了好久的文章才开始分析调试java的cc链,这个链算是java反序列化漏洞里的基础了.分析调试的shiro也是直接使用了cc链.首先先了解一些 ...
- 一本通 高手训练 1788 爬山 dp 斜率 凸包
LINK:爬山 很早以前看的题目 发现自己想的完全不对 这道题还是比较有价值的. 先不考虑走的路线问题 考虑某个点能看到的最高的山. 分左边和右边来考虑 考虑左边 利用单调栈存长度单调递减的山 不能直 ...
