使用pca/lda降维

PCA主成分分析

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 用鸢尾花数据集 展示 降维的效果
from sklearn.datasets import load_iris
iris = load_iris()
data = iris.data  # 特征值
target = iris.target # 目标值
# 绘制平面散点图
plt.scatter(data[:,0],data[:,1],c=target)# 如果要想分类准确 需要考虑所有特征
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(data,target,test_size=0.1)
from sklearn.neighbors import KNeighborsClassifier
X_train,X_test,y_train,y_test = train_test_split(data,target,test_size=0.1)
KNeighborsClassifier().fit(X_train,y_train).score(X_test,y_test)

如果只是打分一次 会有很多偶然因素
所以 应该 做交叉验证

# 定义一个函数 调用函数 传入 模型 数据集的特征值和目标值
# 函数内部会按照 多个比例 对数据集进行切分 然后获取平均分
def cross_verify(model,data,target):
    scores = []
    # 按照不同比例去切分 训练集 和 测试集
    for i in np.arange(0.1,0.2,0.01):
        X_train,X_test,y_train,y_test = train_test_split(data,target,test_size=i)
        score = model.fit(X_train,y_train).score(X_test,y_test)
        # 把每次打分 加入到分数列表中
        scores.append(score)

    return np.array(scores).mean()
cross_verify(KNeighborsClassifier(),data,target)  # 94-97之间 # 0.981

使用PCA来对数据进行降维

# decomposition 分解
from sklearn.decomposition import PCA
# 获取
# n_components 用来控制保留多少个特征 可以传入整数表示保留特征的个数 还可以传入小数表示保留的特征的比例
pca = PCA(n_components=2)
# 训练模型
pca.fit(data)  # pca只是找当前数据自身内部的最大差异 不关心各种分类之间的差别 所以只传入data即可 target可以不传
data.shape  # 150个样本 4个特征
# 对高维度的数据 进行降维 转换
pca_data = pca.transform(data)
# pca.fit_transform
pca_data.shape  # 样本还是原来的样本 只是特征从4个压缩到了2个

对比散点图

plt.scatter(data[:,0],data[:,1],c=target)

plt.scatter(pca_data[:,0],pca_data[:,1],c=target)

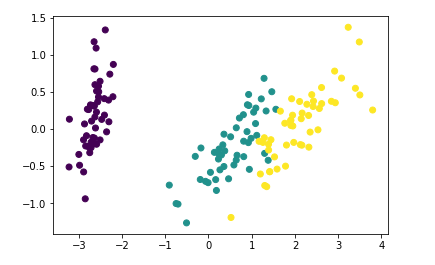
cross_verify(KNeighborsClassifier(),pca_data,target)  # 降低维度是否会影响准确率呢 95-97 大部分情况下降维并不会影响准确率 而且会提高速度

LDA

# discriminant_analysis判别分析
# 线性判别分析 LinearDiscriminantAnalysis
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(data,target)  # lda是要查看 各个分类之间的差异 所以需要传入各个样本的分类的目标值
lda_data = lda.transform(data)
# lda.fit_transform

对比散点图

plt.scatter(pca_data[:,0],pca_data[:,1],c=target)

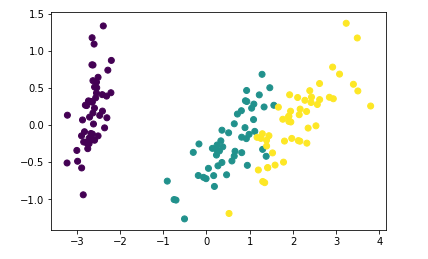
plt.scatter(lda_data[:,0],lda_data[:,1],c=target)

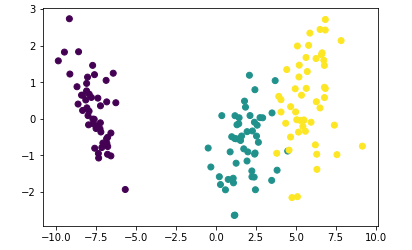
cross_verify(KNeighborsClassifier(),lda_data,target)  # 使用lda进行降维 也不会对准确率产生很大影响