BZOJ3424 : Poi2013 Multidrink

详细做法以及证明请看论文《Hamiltonian paths in the square of a tree》。

首先将1到n的路径提取出来，作为主干。

定义毛毛虫为去掉叶子之后只有一条单链的树，定义non-trivial的毛毛虫为单链非空的毛毛虫。

对于主干上每个点，计算它的非主干部分是否是毛毛虫，如果某个部分不是毛毛虫，那么肯定无解。

将主干上每个点划分为两类：

A：non-trivial的毛毛虫不超过1个。

B：non-trivial的毛毛虫恰有两个。

同时定义一个点是free的当且仅当它是单点。

如下图：

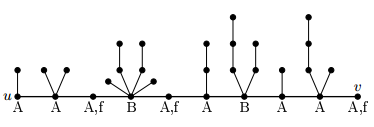
判断一下是否每对相邻的B类点中间都有free点，且所有B类点前后都有free点，如果没有，那么也无解。

现在必然存在一条以1为起点，且依次遍历完主干上每个点及其子树的2H-哈密顿路径。

对于1，如果它是free的，那么方案显然，否则从1出去的点必定是它子树里离它距离只有1的点。

然后一个一个构造，如果上一个点是第二层的点，那么这一部分起点必须为主干上的点，否则起点选第二层的点显然更优。

对于一个毛毛虫，可以直接构造出2H-哈密顿环，从中断开某条路径得到合法的方案。

如下图：

但是如果一个点是B类点，这个时候是不能如此构造的，只能是起点和终点都是第二层的点，而且起点优先考虑叶子节点，这个时候就又可以按之前的方法构造。

最后再检验一下终点是否为n即可，时间复杂度$O(n)$。

#include<cstdio>
#include<cstdlib>
#define N 500010
int n,i,j,x,y,S,T,d[N],g[N],v[N<<1],nxt[N<<1],ed,pre[N],sub[N];
int f[N],G[N],V[N],NXT[N];
int m,a[N],ans,fin[N],cnt,q[N],b[N<<1],tot;bool vip[N],fr[N];
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
void NO(){puts("BRAK");std::exit(0);}
inline void swap(int&a,int&b){int c=a;a=b;b=c;}
inline void reserve(int*a,int n){for(int i=1,j=n;i<j;i++,j--)swap(a[i],a[j]);}
inline void add(int x,int y){d[x]++;v[++ed]=y;nxt[ed]=g[x];g[x]=ed;}
inline void ADD(int x,int y){f[y]=x;V[++ed]=y;NXT[ed]=G[x];G[x]=ed;}
void dfs(int x,int y){
  pre[x]=y;
  for(int i=g[x];i;i=nxt[i])if(v[i]!=y)dfs(v[i],x);
}
bool spine(int x,int y){
  int t=0;
  for(int i=g[x];i;i=nxt[i])if(v[i]!=y&&d[v[i]]>1){
    if(!spine(v[i],x))return 0;
    if(t++)return 0;
  }
  return 1;
}
inline int any_secondary_node(int x){
  for(int i=g[x];i;i=nxt[i])if(!vip[v[i]])return v[i];
}
inline int a_secondary_node_preferably_leaf(int x){
  for(int i=g[x];i;i=nxt[i])if(!vip[v[i]]&&d[v[i]]==1)return v[i];
  return any_secondary_node(x);
}
inline int another_secondary_node(int x,int y){
  for(int i=g[x];i;i=nxt[i])if(!vip[v[i]]&&v[i]!=y)return v[i];
}
void findspine(int x,int y){
  q[++cnt]=x;
  for(int i=g[x];i;i=nxt[i])if(v[i]!=y)if(d[v[i]]==1)ADD(x,v[i]);else findspine(v[i],x);
}
inline int left(int x){return x==1?tot:x-1;}
inline int right(int x){return x==tot?1:x+1;}
inline void extend(int x,int a=0,int b=0){
  for(int i=G[x];i;i=NXT[i])if(V[i]!=a&&V[i]!=b)fin[++ans]=V[i];
}
inline void path_caterpillar(int x,int S,int T){
  fin[++ans]=S;
  if(S==T)return;
  int i,j,A,B;
  q[cnt=1]=x;
  for(i=g[x];i;i=nxt[i])if(!vip[v[i]]){
    if(d[v[i]]==1)ADD(x,v[i]);
    else{
      if(cnt>1)reserve(q,cnt);
      findspine(v[i],x);
    }
  }
  for(i=1;i<=cnt;i++){
    b[i]=i&1?q[i]:-q[i];
    b[cnt+cnt-i+1]=-b[i];
  }
  for(tot=0,i=1;i<=cnt+cnt;i++){
    if(b[i]<0)if(!G[-b[i]])continue;
    b[++tot]=b[i];
  }
  if(d[S]>1)A=S;else A=-f[S];
  if(d[T]>1)B=T;else B=-f[T];
  for(i=1;i<=tot;i++)if(b[i]==A)break;
  if(A<0)extend(-A,S,T);
  if(b[left(i)]==B)
    for(j=right(i);b[j]!=B;j=right(j))if(b[j]>0)fin[++ans]=b[j];else extend(-b[j]);
  else
    for(j=left(i);b[j]!=B;j=left(j))if(b[j]>0)fin[++ans]=b[j];else extend(-b[j]);
  if(B<0&&A!=B)extend(-B,S,T);
  fin[++ans]=T;
}
int main(){
  read(n);
  for(i=1;i<n;i++)read(x),read(y),add(x,y),add(y,x);
  dfs(n,ed=0);
  for(i=1;i!=n;i=pre[i])a[++m]=i;a[++m]=i;
  for(i=1;i<=m;i++)vip[a[i]]=1;
  for(i=1;i<=m;i++){
    x=a[i];fr[x]=1;
    for(j=g[x];j;j=nxt[j]){
      y=v[j];
      if(vip[y])continue;
      fr[x]=0;
      if(d[y]==1)continue;
      sub[x]++;
      if(sub[x]>2)NO();
      if(!spine(y,x))NO();
    }
  }
  for(i=1,j=0;i<=m;i++){
    x=a[i];
    if(fr[x])j=1;
    else if(sub[x]==2){
      if(j!=1)NO();
      j=2;
    }
  }
  if(j==2)NO();
  S=a[1];
  if(fr[a[1]])T=a[1];else T=any_secondary_node(a[1]);
  path_caterpillar(a[1],S,T);
  for(i=2;i<=m;i++){
    x=a[i];
    if(fr[x])S=T=x;
    else if(!vip[T]){
      S=x;
      T=a_secondary_node_preferably_leaf(x);
    }else{
      S=a_secondary_node_preferably_leaf(x);
      T=sub[x]<2?x:another_secondary_node(x,S);
    }
    path_caterpillar(x,S,T);
  }
  if(fin[n]!=n)NO();
  for(i=1;i<=n;i++)printf("%d\n",fin[i]);
  return 0;
}