[洛谷P2785] 物理1(phsic1)-磁通量

随便翻到的一道题......

题目传送门

这道题是用向量叉积求多边形面积。

首先讲一下向量叉积（也叫外积）。

设两个向量的坐标表示为(x1,y1)、(x2,y2)。

那么它们的叉积为x1*y2-x2*y1。

其几何意义为两个向量所成的平行四边形的面积（浅蓝色部分）。

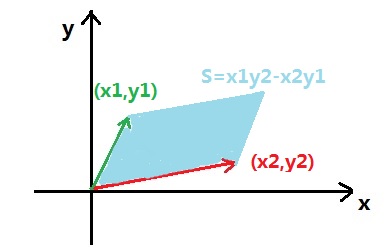
两个向量的叉积与这两个向量都垂直，且有正负之分。

叉积的正负取决于两向量夹角sin值的正负（图中叉积均为：绿向量×红向量）。

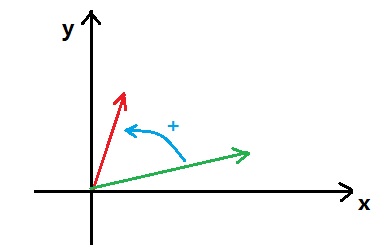
对于两个点A、B以及原点O，向量OA与向量OB的叉积的一半代表三角形OAB的面积。

这样我们就能通过这个把多边形分割成三角形，进而求出多边形的面积。

对于下面这个四边形ABCD：

S(ABCD)=S(OAB)+S(OBC)-S(OCD)-S(ODA)。

我们沿着多边形走一周，依次加上（或减掉）相邻的两个顶点与原点形成的三角形的面积就行。

三角形的面积就用叉积算嘛。

而且你可以发现向量的叉积特别可爱，都不需要你判断是该加上还是该减掉。

叉积算出来是正的，对面积的贡献就为正；是负的，对面积的贡献就为负。

最后别忘了最后一个点和第一个点也要求一下叉积。

所以多边形的面积就这么愉快地算出来啦~

 #include<cstdio>

 int n;
 double b,ans;

 struct vec
 {
     double x,y;
 }a[];

 double cross(vec q,vec w)
 {
     return q.x*w.y-w.x*q.y;
 }

 int main()
 {
     scanf("%d%lf",&n,&b);
     for(int i=;i<=n;i++)scanf("%lf%lf",&a[i].x,&a[i].y);
     a[n+]=a[];
     for(int i=;i<=n;i++)ans+=cross(a[i],a[i+]);
     ans=ans*b*0.50;
     if(ans<)ans=-ans;
     printf("%.4lf",ans);
     return ;
 }