POJ 1039：Pipe 计算几何

Pipe

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 9773		Accepted: 2984

Description

The GX Light Pipeline Company started to prepare bent pipes for the new transgalactic light pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside each component of the pipe.
Note that the material which the pipe is made from is not transparent and not light reflecting. 




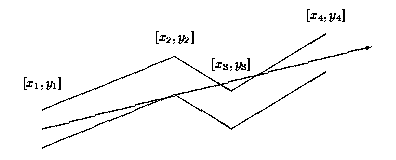
Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These
are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find,
for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent
points and the bent points do not stop the light beam.

Input

The input file contains several blocks each describing one pipe component. Each block starts with the number of bent points 2 <= n <= 20 on separate line. Each of the next n lines contains a pair of real values xi, yi separated by space. The last block is denoted
with n = 0.

Output

The output file contains lines corresponding to blocks in input file. To each block in the input file there is one line in the output file. Each such line contains either a real value, written with precision of two decimal places, or the message Through all
the pipe.. The real value is the desired maximal x-coordinate of the point where the light can reach from the source for corresponding pipe component. If this value equals to xn, then the message Through all the pipe. will appear in the output file.

Sample Input

4
0 1
2 2
4 1
6 4
6
0 1
2 -0.6
5 -4.45
7 -5.57
12 -10.8
17 -16.55
0

Sample Output

4.67
Through all the pipe.

有一个分成几节的水管，水管用上端的断点表示出来，下端与上端断点的距离固定是1。该水管不反射光线，问所有射入该水管的光线中 能到达的最远距离是多少。如果能穿越整个水管，输出Through all the pipe。

套用黑书里面的话。

如果一根光线自始至终未擦到任何顶点，肯定不是最优的(可以通过平移使之优化)。然后，如果只碰到一个顶点，那也不是最优的，可以通过旋转，使它碰到另一个顶点，并且更优。所以最优光线必然是擦到一个上顶点和一个下顶点。其中每一步都是根据目前阻挡光线的管壁的方向，选择使光线更优的操作。

于是有了一个简单的算法，任取一个上顶点和下顶点，形成直线l。若l能射穿左入口，即当x=x0时，直线l在(x0,y0)和(x0,y0 - 1)之间，则是一条可行光线。再从左到右依次判断每条上、下管壁是否与l相交，相交则求交点，并把焦点x值与当前最佳值进行比较，若所有管壁都不与l相交，说明l射穿了整个管道。

代码：

#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
#include <string>
#include <cstring>
#include <iomanip>
#pragma warning(disable:4996)
using namespace std;

struct point
{
	double x, y;
}up[22],down[22];
const double eps = 1e-3;

//叉积
double Multi(point p1, point p2, point p0)
{
	return (p1.x - p0.x)*(p2.y - p0.y) - (p2.x - p0.x)*(p1.y - p0.y);
}

//直线ab与线段cd是否相交
bool Across(point a, point b, point c, point d)
{
	double tmp = Multi(c, a, b)*Multi(d, a, b);
	if (tmp < 0 || fabs(tmp) < eps)
		return true;
	else
		return false;
}

//求两条直线的交点坐标
double getIntersect(point a, point b, point c, point d)
{
	double A1 = b.y - a.y;
	double B1 = a.x - b.x;
	double C1 = (b.x - a.x)*a.y - (b.y - a.y)*a.x;
	double A2 = d.y - c.y;
	double B2 = c.x - d.x;
	double C2 = (d.x - c.x)*c.y - (d.y - c.y)*c.x;
	double x = (C2*B1 - C1*B2) / (A1*B2 - A2*B1);
	double y = (C1*A2 - C2*A1) / (A1*B2 - A2*B1);

	return x;
}

int main()
{
	int n, i, j, k;
	double res;
	bool flag;

	while (scanf("%d", &n) && n)
	{
		for (i = 0; i < n; i++)
		{
			scanf("%lf%lf", &up[i].x, &up[i].y);
			down[i].x = up[i].x;
			down[i].y = up[i].y - 1;
		}
		res = up[0].x;
		flag = false;

		for (i = 0; i < n&&!flag; i++)
		{
			for (j = 0; j < n&&!flag; j++)
			{
				if (i == j)continue;
				for (k = 0; k < n; k++)
				{
					if (!Across(up[i], down[j], up[k], down[k]))
						break;
				}
				if (k == n)
				{
					flag = true;
				}
				else if (k > max(i, j))
				{
					res = max(res, getIntersect(up[i], down[j], up[k - 1], up[k]));
					res = max(res, getIntersect(up[i], down[j], down[k - 1], down[k]));
				}
			}
		}
		if (flag)
			cout << "Through all the pipe." << endl;
		else
			cout << fixed << setprecision(2) << res << endl;
	}
	return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。