洛谷——P2296 寻找道路

P2296 寻找道路

题目描述

在有向图G 中，每条边的长度均为1 ，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1 ．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2 ．在满足条件1 的情况下使路径最短。

注意：图G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入输出格式

输入格式：

输入文件名为road .in。

第一行有两个用一个空格隔开的整数n 和m ，表示图有n 个点和m 条边。

接下来的m 行每行2 个整数x 、y ，之间用一个空格隔开，表示有一条边从点x 指向点y 。

最后一行有两个用一个空格隔开的整数s 、t ，表示起点为s ，终点为t 。

输出格式：

输出文件名为road .out 。

输出只有一行，包含一个整数，表示满足题目᧿述的最短路径的长度。如果这样的路径不存在，输出- 1 。

输入输出样例

输入样例#1：

3 2
1 2
2 1
1 3

输出样例#1：

-1

输入样例#2：

6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5

输出样例#2：

3

说明

解释1：

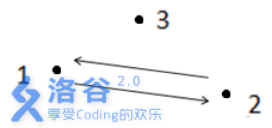
如上图所示，箭头表示有向道路，圆点表示城市。起点1 与终点3 不连通，所以满足题

目᧿述的路径不存在，故输出- 1 。

解释2：

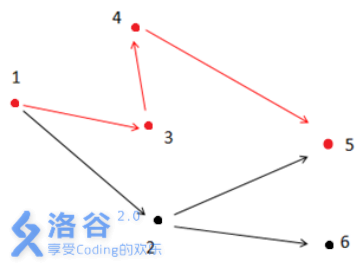
如上图所示，满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中，因为点2连了一条边到点6 ，而点6 不与终点5 连通。

对于30%的数据，0<n≤10，0<m≤20；

对于60%的数据，0<n≤100，0<m≤2000；

对于100%的数据，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

一心的认为这是一道最短路的裸题，结果敲出板子来以后发现样例过不了，然后就开始看下面的图，发现题目中的要求为如果能到达e的点可以到达别的点，但是这个点如果不能到达e那么这条路就不能走，这样的话我们队于愿来的路径建反向边，然后跑一边bfs（注意是bfs，我跑了两次dfs结果T成狗了、、、）找出结尾的点不能到达的点，然后我们这样的点所在的路径是一定不能走的，我们处理出这样的路径以后跑一边spfa，由于我们建是反向边，那么我们倒着跑一遍spfa就好了

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 200100
using namespace std;
queue<int>q;
bool vis[N],vist[N];
int n,m,s,e,x,y,tot,dis[N],head[N];
int read()
{
    ,f=; char ch=getchar();
    ') ch=getchar();
    +ch-'; ch=getchar();}
    return x*f;
}
struct Edge
{
    int to,next;
}edge[N];
int add(int x,int y)
{
    tot++;
    edge[tot].to=y;
    edge[tot].next=head[x];
    head[x]=tot;
}
int spfa(int s)
{
    memset(vis,,sizeof(vis));
    memset(dis,0x3f3f3f3f,sizeof(dis));
    dis[s]=,vis[s]=true;q.push(s);
    while(!q.empty())
    {
        int x=q.front(); q.pop(); vis[x]=false;
        for(int i=head[x];i;i=edge[i].next)
        {
            int to=edge[i].to;
            ||vist[to]) continue;
            dis[to]=dis[x]+;
            if(vis[to]) continue;
            q.push(to);
            vis[to]=true;
        }
    }
}
int bfs(int s)
{
    vis[s]=true;q.push(s);
    while(!q.empty())
    {
        int x=q.front(); q.pop();
        for(int i=head[x];i;i=edge[i].next)
        {
            int to=edge[i].to;
            if(!vis[to]) q.push(to),vis[to]=true;
        }
    }
}
int main()
{
    n=read(),m=read();
    ;i<=m;i++)
     x=read(),y=read(),add(y,x);
    s=read(),e=read();
    bfs(e);
    ;i<=n;i++)
     if(vis[i]==false)
      for(int j=head[i];j;j=edge[j].next)
        vist[edge[j].to]=true;
    ;i<=n;i++)
     if(!vis[i]) vist[i]=true;
    spfa(e);
    if(dis[s]>=0x3f3f3f3f) printf("-1");
    else printf("%d",dis[s]);
    ;
}