18B树、B++树和Trie树
B树、B++树和Trie树
B树
定义:一个非空M元(也称M阶)B树(R.Bayer,1970年)
满足下列条件:
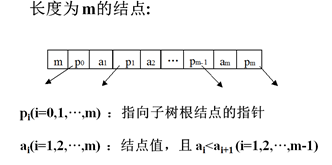
1)每个结点含有m个元素a1<a2<…<am。含有m个元素的结点有m+1个子树,m称为结点长度
2)结点长度m满足:
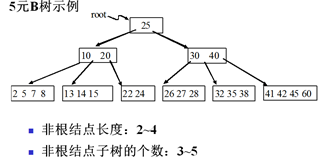
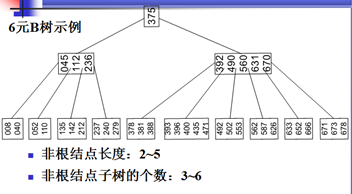
根结点,1≤m≤M-1 可以有2~M个子树
非根结点,M/2-1≤m≤M-1
可以有M/2~M个子树
3)结点结构中:
pi(i=0,1,…,m)是指向第i个子树的指针
ai(i=1,…,m)是结点值
对于非叶结点,第0个子树上所有元素都小于a1
第i个子树上的元素x满足ai<x<ai+1(1≤i≤m-1)
第m个子树上所有元素都大于am
4)所有的叶均在同一层上
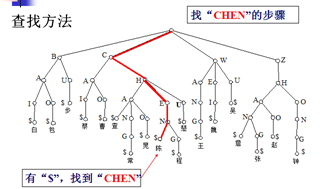
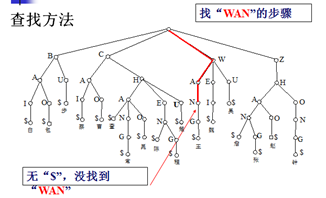
B树的查找
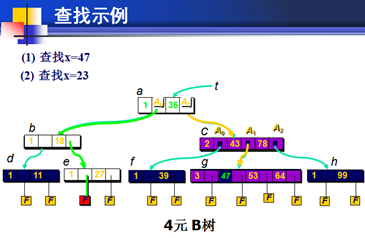
查找元素x的步骤大致如下:
步骤1)如果当前结点为空,则查找失败
步骤2)在当前结点中查找x
如果找到x,查找成功;
否则
若x<a1,沿p0递归向下查找
若ai<x<ai+1(1≤i<m),沿pi递归向下查找
若x>am,沿pm递归向下查找
B树的插入
插入步骤如下:
步骤1)用查找的方法为x找到所在位置,查找路径终止于某个空树,把x插在其父结点的有序位置上
步骤2)如果插入x后,结点不超长,则插入完毕;
否则,进入下一步超长处理
步骤3)将超长结点一分为二,将“中间元素”递归地插在上层结点中
步骤4)若插入波及到根,当根上溢时,把根一分为二,并将中间元素上移,而产生含单元素的新根,使B树升高。
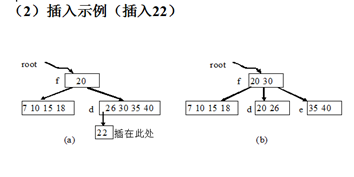
将超长结点d一分为二的操作方法:
1. 超长结点d的元素达M个,令k=M/2,元素ak作为中间元素。
2. 将排在ak左侧的元素和相应的指针被保留在结点d中。
3. 将排在ak右侧的元素和相应的指针移入新结点e中。
4. 将ak连同指向结点e的指针一起插在d的父结点f中,排在指向结点d的指针右侧。
B树的删除
(1)删除x大体步骤:
步骤1)经查找,在某一结点c中找到x
步骤2)根据x所在位置的不同,作出不同的处理
①如果c是叶,直接从叶中删除x
②如果c是非叶,需要用x的“中序前驱”代替x。
注意:
寻找x的中序前驱:
沿着x左侧子树的最右分枝一直下降到某个叶结点s,结点s中最右元素y便是x的前驱,
用y代替x(复制)后,在结点s中删除y。
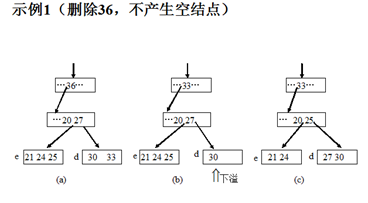
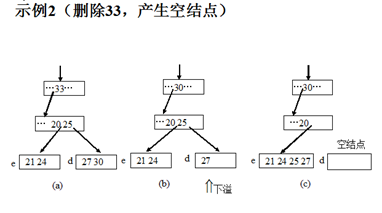
步骤3)如果删除后d(d指的是真正删除元素的结点)不下溢,删除结束;否则,进入下一步下溢处理。
步骤4)如果d是根(根变空才算下溢),转步骤9;否则,进入下一步。
步骤5)找d的邻近兄弟e。(现在d下溢,d不是根,d的长度小于M/2-1)。
步骤6)如果e长度未到下限,即多于半满(否则,进入步骤7) ,则从e中借一个元素(连同相应的指针)给d,并应适当地调整d和e之间的那个元素,删除结束。
步骤7)将e合并到d,也就是把e中的元素,以及d和e之父f的那个“中间元素”都加到结点d中,结点e变空,删除空结点e。(也可将d合并到e,而删除d)。
步骤8)如果引起f下溢,令d=f转步骤4;否则删除结束。(因f的元素下移,使f的长度减小)
步骤9)(根的长度变为0)删除根,B树高度下降。
B+树
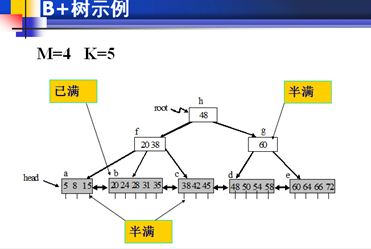
基本概念
(1)B+树与B树主要区别:
所有的数据元素都存储在叶结点中,非叶结点仅存便于查找的索引信息(索引结点)。
1)第i个子树上的元素x满足ai<x≤ai+1可取等号,与B树不同。
2)叶与非叶具有不同的结点结构。叶结点中可以存放储K/2~K个元素;K的可以与树的元数M相等也可以不等。
注意点:
将叶结点“穿成”有序链表。具有“两套”查找机构。
纵向:沿树枝进行查找;
横向:沿链表顺序查找。
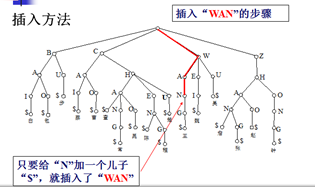
B+树的插入
(1)插入x的大体步骤:
步骤1)从根结点起,沿纵向搜索路径为x找到所在的叶结点d。如果叶d未满,则把x插在叶d的有序位置上,插入完毕;否则,进入下一步。
步骤2)叶d已满,叶长达到K,将d一分为二:
产生新叶e,将d的下部K/2个元素移入e,另一半留在d中。
设d的父亲是f,给f加一个儿子e,e排在d之右侧,将e的最小元素的值加到f中作为新索引项,如果f不超长,则插入结束;否则,进入下一步。
步骤3)将f分裂成f和g,并递归地将g插到上一层中。
步骤4)若插入波及到根,当根上溢时,把根一分为二,并产生新根。
B+树的插入示例:


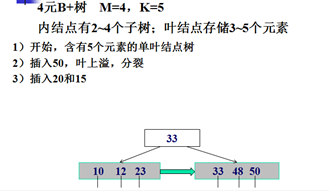
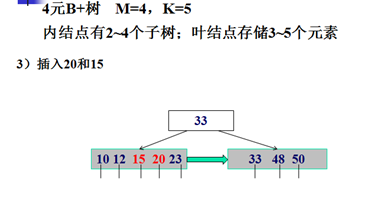
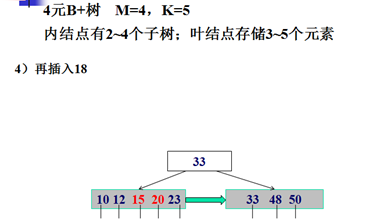
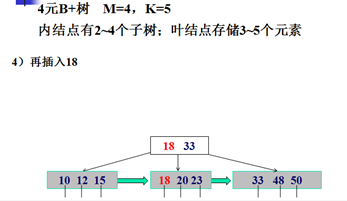

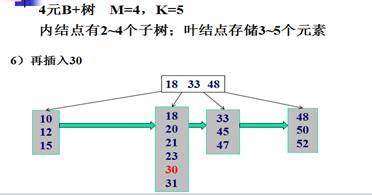
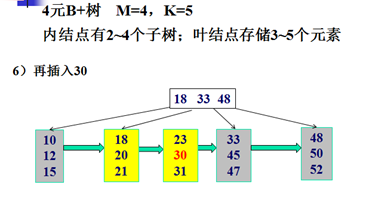
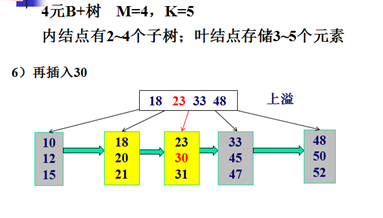
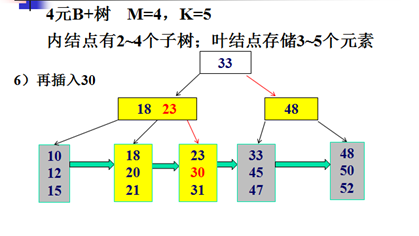
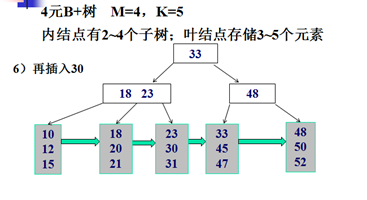
B+树的删除
(1)删除x的大体步骤:
步骤1)沿根到某叶的一条路径查找x,如果x不存在,删除失败,结束;否则,进入下一步。
步骤2)在x所在叶d中删除x。如果删除x后,叶d不下溢,则删除结束;否则,进入下一步。
步骤3)找叶d的兄弟e。如果e处于半满状态,进入步骤4;
否则,从e中移一个元素给叶d。如果e在d的左侧,则移的是e中最大元素;如果e在d的右侧,则移的是e中最小元素,移走元素的同时,修改上层结点中的索引信息,删除结束。
步骤4)将d合并到e。将d的所有元素都给e,删除d,并相应的修改上层结点中的索引信息,也可将e合并到d。
步骤5)如果删除d不引起其父f的下溢,则删除结束;
否则,将递归地波及到更上层结点,或者可以向其兄弟“借”一个索引项和一个子树,或者与其兄弟合并。如果波及根,根长度为0,删除根,整个树的高度下降,删除非叶结点的大体步骤与B树相同。
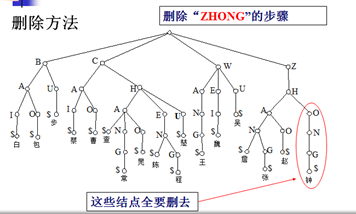
删除示例:
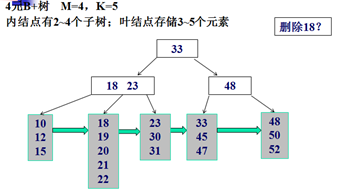
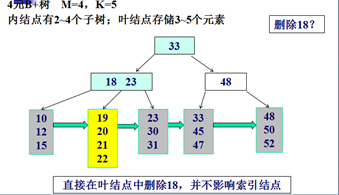
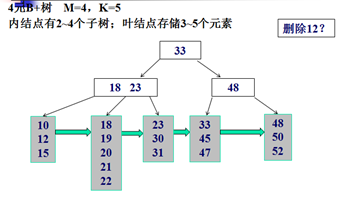
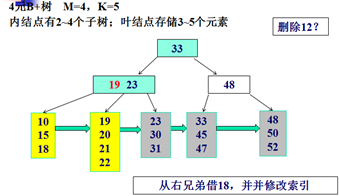
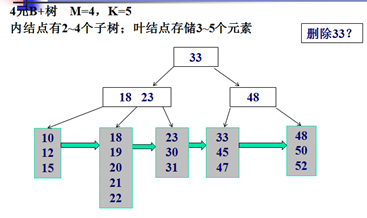
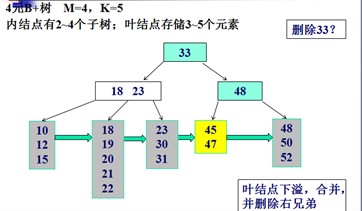
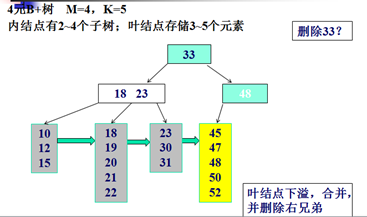
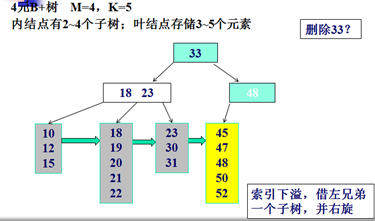
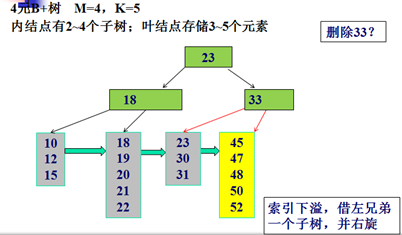
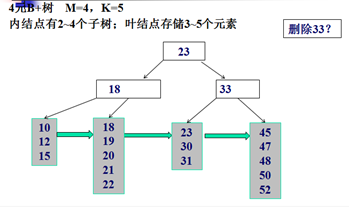
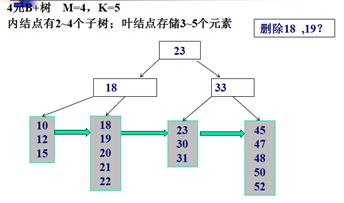
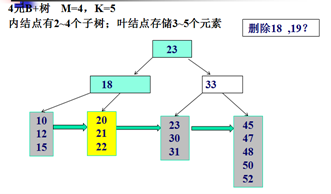
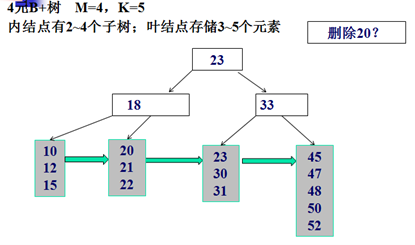
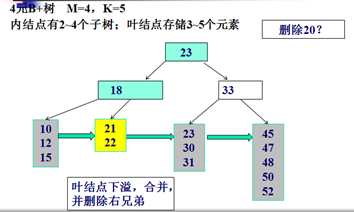
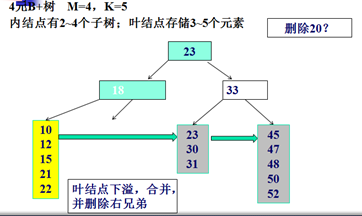
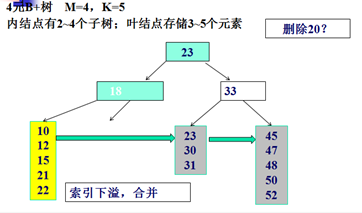
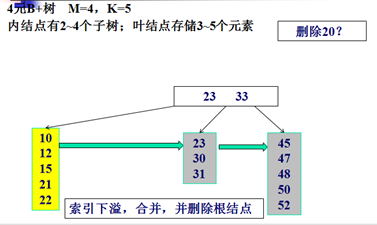
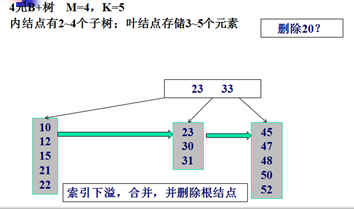
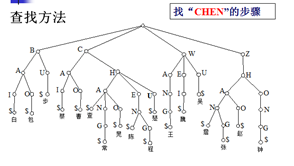
Trie树
组织结构:
定义:属于数字查找树,用于按数字或字符索引。像大型字典的“书边标目”。
优点:
1.元素(字符串)存储在叶结点中。
2.非叶结点只存储一个字符作为索引。
3.从根到某个叶的路径上字符组合成的字符串,恰是存储于该叶中的元素值(关键字)。
示例:
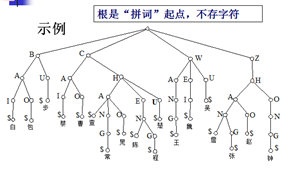
18B树、B++树和Trie树的更多相关文章
- 从Trie树到双数组Trie树
Trie树 原理 又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种.它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,能在常数时间O(len)内实现插入和查 ...
- python Trie树和双数组TRIE树的实现. 拥有3个功能:插入,删除,给前缀智能找到所有能匹配的单词
#coding=utf- #字典嵌套牛逼,别人写的,这样每一层非常多的东西,搜索就快了,树高26.所以整体搜索一个不关多大的单词表 #还是O(). ''' Python 字典 setdefault() ...
- [FJOI2015]火星商店问题(线段树分治,可持久化,Trie树)
[FJOI2015]火星商店问题 前天考了到线段树分治模板题,全场都切了,就我不会QAQ 于是切题无数的Tyher巨巨就告诉我:"你可以去看看火星商店问题,看了你就会了." 第一道 ...
- Trie树的应用:查询IP地址的ISP
1. 问题描述 给定一个IP地址,如何查询其所属的ISP,如:中国移动(ChinaMobile),中国电信(ChinaTelecom),中国铁通(ChinaTietong)?现有ISP的IP地址区段可 ...
- 字典树(Trie树)的实现及应用
>>字典树的概念 Trie树,又称字典树,单词查找树或者前缀树,是一种用于快速检索的多叉树结构,如英文字母的字典树是一个26叉树,数字的字典树是一个10叉树.与二叉查找树不同,Trie树的 ...
- trie树(前缀树)
问题描述: Trie树,即字典树,又称单词查找树或键树,是一种树形结构,是一种哈希树的变种.典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计.它的优 ...
- 双数组Trie树 (Double-array Trie) 及其应用
双数组Trie树(Double-array Trie, DAT)是由三个日本人提出的一种Trie树的高效实现 [1],兼顾了查询效率与空间存储.Ansj便是用DAT(虽然作者宣称是三数组Trie树,但 ...
- 【动画】看动画轻松理解「Trie树」
Trie树 Trie这个名字取自“retrieval”,检索,因为Trie可以只用一个前缀便可以在一部字典中找到想要的单词. 虽然发音与「Tree」一致,但为了将这种 字典树 与 普通二叉树 以示区别 ...
- Codeforces 861D - Polycarp's phone book 【Trie树】
<题目链接> 题目大意: 输入7e4个长度为9的字符串,每个字符串中只出现0~9这几种数字,现在需要你输出每个母串中最短的特有子串. 解题分析: 利用Trie树进行公共子串的判定,因为Tr ...
- 从Trie树(字典树)谈到后缀树
转:http://blog.csdn.net/v_july_v/article/details/6897097 引言 常关注本blog的读者朋友想必看过此篇文章:从B树.B+树.B*树谈到R 树,这次 ...
随机推荐
- 替换linux系统文件etc下passwd文件的字段获取真正的root权限
sudo与root 很多人都知道使用linux可以利用sudo来执行一些root权限执行的事情,但是sudo和root还是有很大的区别的. 区别一:sudo可以执行的命令是root账户利用/etc/s ...
- Mac下一款门罗币挖矿木马的简要分析
背景 最近在应急中发现了一款Mac上的挖矿木马,目标是挖门罗币,经过走访,受害用户都有从苹果电脑上安装第三方dmg的经历(其中可以确定一款LOL Mac私服安装app会导致该木马),怀疑在网上很多第三 ...
- DragonBones龙骨发布后在Egret中的位置
DragonBones发布后的动画,加载到Egret中场景中,原点的位置在哪呢? DragonBones中的图片位置 导出 加载到Egret中.可见DragonBones中的图片位置原点左下方(0,0 ...
- 23种设计模式之享元模式(FlyWeight)
享元模式是一种对象结构型模式,通过运用共享技术,有效地支持大量细粒度的对象.系统只使用少量的对象,而这些对象都很相似,状态变化很小,对象使用次数增多.享元对象能做到共享的关键是区分内部状态和外部状态. ...
- python nose测试框架中使用allure_report框架
在使用nose自带的xunit生成xml文件生成测试报告后,领导说报告不够炫,没有百分比效果,且在web自动化时的截图不美观,html很多情况下没有显示图片(nose框架截图方法这里),正好,allu ...
- git如何回滚当前修改的内容?
git如何回滚当前修改的内容? 1.打开git gui,在工具栏上点击 commit ,选择 Revert Changes, 这里可以回滚单个文件: 2.一键回滚所有修改: 打开git gui,在工 ...
- java8新特性之Optional类
NullPointException可以说是所有java程序员都遇到过的一个异常,虽然java从设计之初就力图让程序员脱离指针的苦海,但是指针确实是实际存在的,而java设计者也只能是让指针在java ...
- java-04-动手动脑
1String.equals()方法的实现代码 public boolean equals(Object anObject) { if (this == anObject) { return true ...
- VS2015 中使用 MVC4
最近把机子升级到win10 觉得还是好用, 又看了一个vs最新版,于时就安了个vs2015 可以前MVC4的项目用不起了 System.Web.Mvc这个有叹号,生成还要报错, 看了一下原因找不到4. ...
- poj1001 Exponentiation【java大数】
Exponentiation Time Limit: 500MS Memory Limit: 10000K Total Submissions: 183034 Accepted: 44062 ...
