【KAWAKO】DTLN-1Dconv的原理

前言
怎么理解DTLN的第二部分呢
对1D卷积的具体理解
1D卷积相较于STFT的优缺点
- 优点
- 缺点（不太确定）
参考文献

前言

DTLN是一种能够实时处理的语音降噪算法，其开源代码在这里，论文在这里。

DTLN的结构如上图，其结构分为两个部分。第一部分（上图左边）是在stft得到的频谱上进行降噪处理，属于频域处理。第二部分（上图右边）是在1D卷积得到的特征上进行进一步降噪处理，也属于频域处理。

其网络结构部分的源码如下。两个1D卷积已用红框标出。

可以注意到，两个1D卷积的参数如下：

第一个1D卷积，输入维度为11512（32ms），卷积核的大小为1*1、个数为encoder_size=256，步长为1，无bias。
第二个1D卷积，输入维度为11256，卷积核的大小为1*1、个数为blocklen=512，步长为1，无bias。

怎么理解DTLN的第二部分呢

第一部分进行降噪处理后，将处理过后的频谱进行傅里叶反变换，得到了长度为512（32ms）的时域信息。
第二部分的第一个1D卷积对长度为512（32ms）的时域信息进行卷积，又得到了256维的频域信息。该操作与stft类似，都是512/2（但是没+1），不同的是stft的到的频点是平均分布的，而1D卷积得到的频点分布是网络学习出来的（可能有的地方频点分布疏，有的地方频点分布密）。网络学习得到的频点分布（应该）更能适应不同的任务。
对1D卷积得到的频域信息进行归一化以后过一遍LTSM+FC+Sigmoid，得到相对于1D卷积学习到的频点分布的mask（频带增益）。
将学习得到的mask与之前1D卷积得到的频域信息相乘，得到降噪处理之后的频域信息。
对降噪处理之后的频域信息进行第二次1D卷积，将256维的频域信息转换回长度为512（32ms）的时域信息，相当于ifft。
对转换回来的长度为512（32ms）的时域信息与前一帧的信息进行overlap-add，最后得到降噪后的声音。

对1D卷积的具体理解

encoded_frames = Conv1D(self.encoder_size,1,strides=1,use_bias=False)(estimated_frames_1)

拿第一个1D卷积举例。卷积核的数量是encoder_size=256，卷积核大小是11，步长是1。其输入是11512的时域信息，输出是11*256的频域信息。

与二维卷积的计算方法相同，其参数量为

(kernel_width * kernel_height * input_channels + bias_num) * output_channels

将时域信息的512个采样点理解为通道数，则卷积的参数量为(11512+0)*256。矩阵乘法如下图。

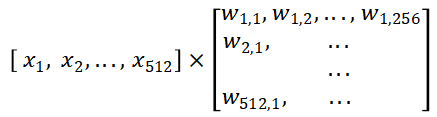
其中Xn为时域信息的第n个采样点，Wn,c为第c个卷积核（也就是频点）在第n个采样点上的权重。矩阵相乘时，X行向量与W矩阵的第c列进行相乘相加，得到的就是在第c个频点上的能量值。因此W矩阵的c个列就代表c个采样点，刚好与512个采样点的一半所对应。

1D卷积相较于STFT的优缺点

优点

相较于STFT的平均分布频点，1D卷积可以通过网络学习到更合适的频点分布。

缺点（不太确定）

1D卷积的计算量比STFT高。

1D卷积的计算量为：

kernel_width * kernel_height * input_channels * output_width * output_height * output_channels

在本案例中即为：1151211*256 = 131072

参考这篇博客，在窗宽度为512上进行fft的计算量为：(np.log2(512)512/2+np.log2(512)512)*9 = 62208

可以看到stft的计算量比1D卷积小。

参考文献

语音分离技术博客

TASNET

Conv-TasNet