boxcox1p归一化+pipeline+StackingCVRegressor

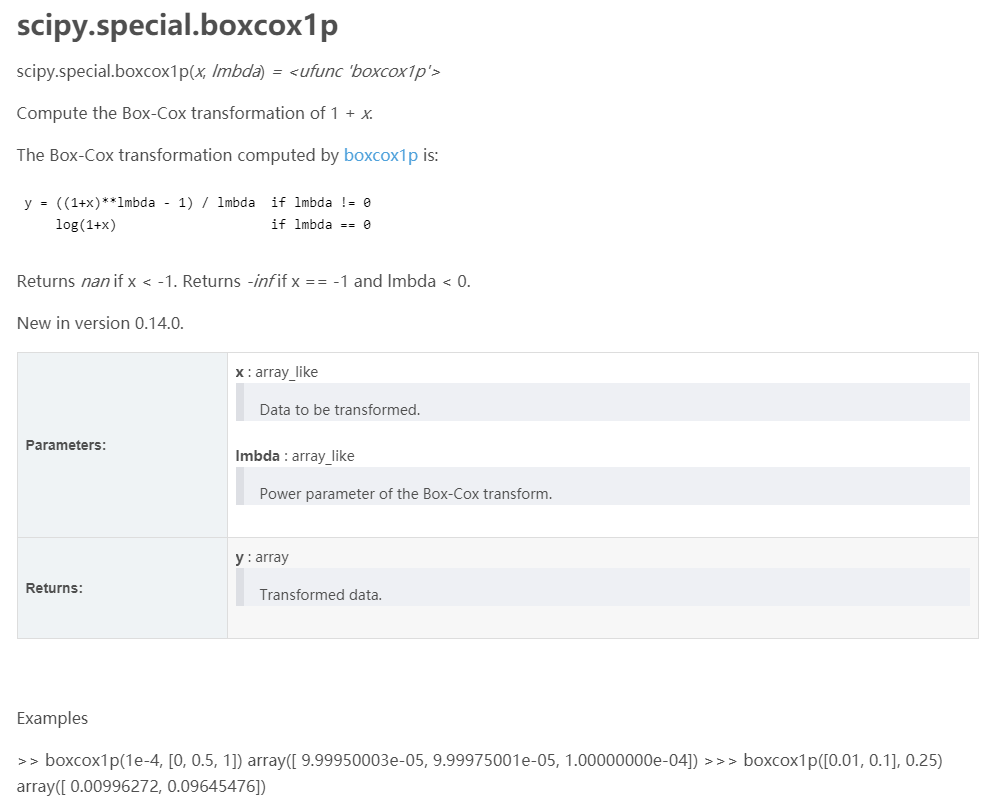
找到最好的那个参数lmbda。

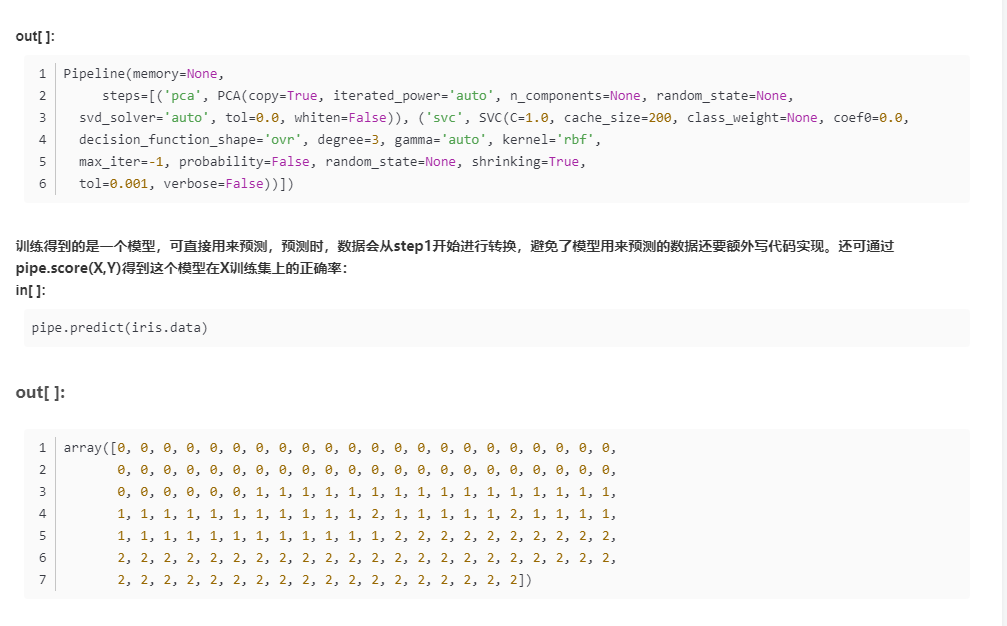
from mlxtend.regressor import StackingCVRegressor
from sklearn.datasets import load_boston
from sklearn.svm import SVR
from sklearn.linear_model import Lasso
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score
import numpy as np
RANDOM_SEED = 42
X, y = load_boston(return_X_y=True)
svr = SVR(kernel='linear')
lasso = Lasso()
rf = RandomForestRegressor(n_estimators=5,
random_state=RANDOM_SEED)
# The StackingCVRegressor uses scikit-learn's check_cv
# internally, which doesn't support a random seed. Thus
# NumPy's random seed need to be specified explicitely for
# deterministic behavior
np.random.seed(RANDOM_SEED)
stack = StackingCVRegressor(regressors=(svr, lasso, rf),
meta_regressor=lasso)
print('5-fold cross validation scores:\n')
for clf, label in zip([svr, lasso, rf, stack], ['SVM', 'Lasso','Random Forest','StackingClassifier']):
scores = cross_val_score(clf, X, y, cv=5)
print("R^2 Score: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
5-fold cross validation scores:
R^2 Score: 0.45 (+/- 0.29) [SVM]
R^2 Score: 0.43 (+/- 0.14) [Lasso]
R^2 Score: 0.52 (+/- 0.28) [Random Forest]
R^2 Score: 0.58 (+/- 0.24) [StackingClassifier]
# The StackingCVRegressor uses scikit-learn's check_cv
# internally, which doesn't support a random seed. Thus
# NumPy's random seed need to be specified explicitely for
# deterministic behavior
np.random.seed(RANDOM_SEED)
stack = StackingCVRegressor(regressors=(svr, lasso, rf),
meta_regressor=lasso)
print('5-fold cross validation scores:\n')
for clf, label in zip([svr, lasso, rf, stack], ['SVM', 'Lasso','Random Forest','StackingClassifier']):
scores = cross_val_score(clf, X, y, cv=5, scoring='neg_mean_squared_error')
print("Neg. MSE Score: %0.2f (+/- %0.2f) [%s]"

from mlxtend.regressor import StackingCVRegressor
from sklearn.datasets import load_boston
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import GridSearchCV
X, y = load_boston(return_X_y=True)
ridge = Ridge()
lasso = Lasso()
rf = RandomForestRegressor(random_state=RANDOM_SEED)
# The StackingCVRegressor uses scikit-learn's check_cv
# internally, which doesn't support a random seed. Thus
# NumPy's random seed need to be specified explicitely for
# deterministic behavior
np.random.seed(RANDOM_SEED)

stack = StackingCVRegressor(regressors=(lasso, ridge),
                            meta_regressor=rf,
                            use_features_in_secondary=True)
params = {'lasso__alpha': [0.1, 1.0, 10.0],
          'ridge__alpha': [0.1, 1.0, 10.0]}

grid = GridSearchCV(
                  estimator=stack,param_grid={'lasso__alpha': [x/5.0 for x in range(1, 10)],
                'ridge__alpha': [x/20.0 for x in range(1, 10)],
                'meta-randomforestregressor__n_estimators': [10,100]},
    cv=5,
    refit=True
)

grid.fit(X, y)

print("Best: %f using %s" % (grid.best_score_, grid.best_params_))

#Best: 0.673590 using {'lasso__alpha': 0.4, 'meta-randomforestregressor__n_estimators': 10, 'ridge__alpha

cv_keys = ('mean_test_score', 'std_test_score', 'params')
for r, _ in enumerate(grid.cv_results_['mean_test_score']):
  print("%0.3f +/- %0.2f %r"
          % (grid.cv_results_[cv_keys[0]][r],
          grid.cv_results_[cv_keys[1]][r] / 2.0,
          grid.cv_results_[cv_keys[2]][r]))
  if r > 10:
    break
print('...')

print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)