[POI2008]CLO

Description

Byteotia城市有n个 towns m条双向roads. 每条 road 连接 两个不同的 towns ,没有重复的road. 你要把其中一些road变成单向边使得：每个town都有且只有一个入度

Input

第一行输入n m.1 <= n<= 100000,1 <= m <= 200000 下面M行用于描述M条边.

Output

TAK或者NIE 常做POI的同学,应该知道这两个单词的了...

Sample Input

4 5

1 2

2 3

1 3

3 4

1 4

Sample Output

TAK

HINT



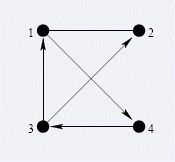
上图给出了一种连接方式.

---

这题可以把边删掉……也就是直接忽略一些边……

那就直接判断，有树就不可行，否则就可行，点也算树。并查集维护一波

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
	int x=0,f=1;char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')    f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x>=10)     print(x/10);
	putchar(x%10+'0');
}
const int N=1e5;
int fa[N+10];
bool can[N+10];
int find(int x){
	if (fa[x]==x)	return x;
	fa[x]=find(fa[x]);
	return fa[x];
}
int main(){
	int n=read(),m=read();
	for (int i=1;i<=n;i++)	fa[i]=i;
	for (int i=1;i<=m;i++){
		int x=find(read()),y=find(read());
		x!=y?(fa[x]=y,can[y]|=can[x]):can[fa[x]]=1;
	}
	for (int i=1;i<=n;i++)	if (!can[find(i)]){printf("NIE\n");return 0;}
	printf("TAK\n");
	return 0;
}