算法竞赛——BFS广度优先搜索

BFS

广度优先搜索：一层一层的搜索（类似于树的层次遍历）

BFS基本框架

基本步骤：

1. 初始状态（起点）加到队列里

2. while(队列不为空)

   队头弹出

   扩展队头元素（邻接节点入队）

3. 最后队为空，结束

BFS难点所在（最短路问题）：

1. 存储的数据结构：队列

   状态如何存储到队列里边（以什么形式）?

2. 状态怎么表示，怎么转移?

3. dist

   如何记录每一个状态的距离

最短路问题：宽搜的优势是能找到最短（最小）路！（所有边权重都一样才可以用！）——一层一层的搜索（类似于树的层次遍历）。深搜可以保证我们走到终点，但不能确保是最短路。

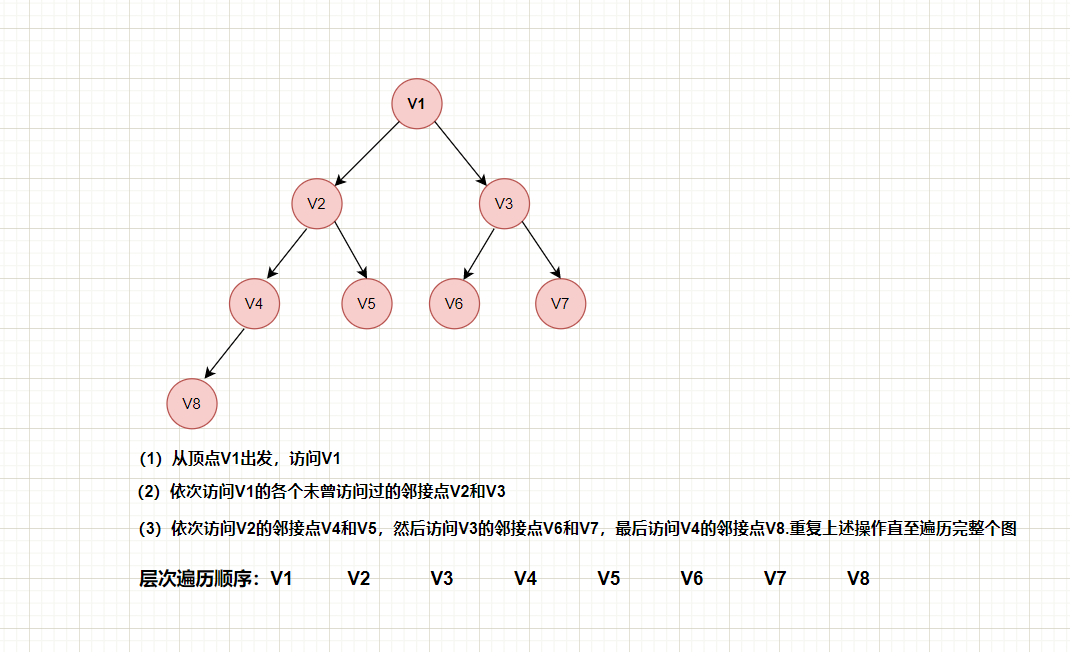
搜索过程（层次遍历）如下：

（1）从图中的某个顶点出V发，访问V

（2）依次访问V的各个未曾访问过的邻接点

（3）分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问

（4）重复步骤（3）直至所有已被访问的顶点的邻接点都被访问到

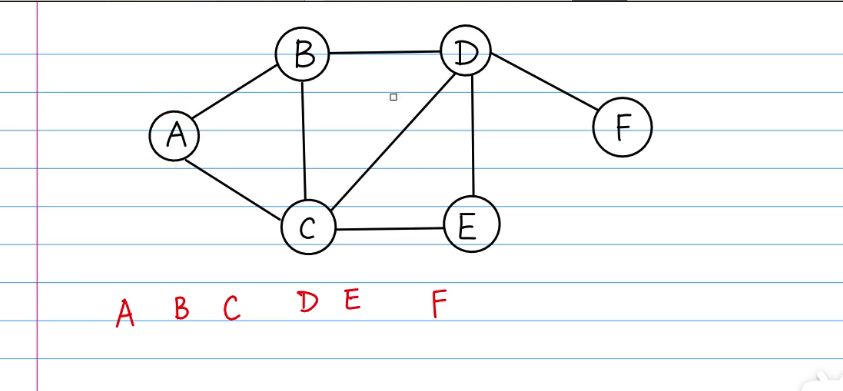
图的BFS和树几乎一模一样，唯一的区别是树有根节点，而图没有，因此在遍历图时要选一个根节点。下图以A作为根节点：

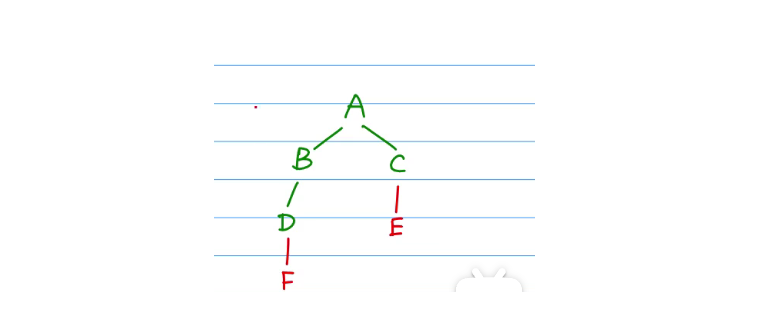
D和E是不能颠倒过来的，因为我们先遍历到的顶点是B，下一次展开的时候必须找与B直接相连的节点，即必须在找与C相连的节点之前把所有与B相连的节点找出来，由于A和C都走过了，因此唯一能走的点就是D。因此B先走完！

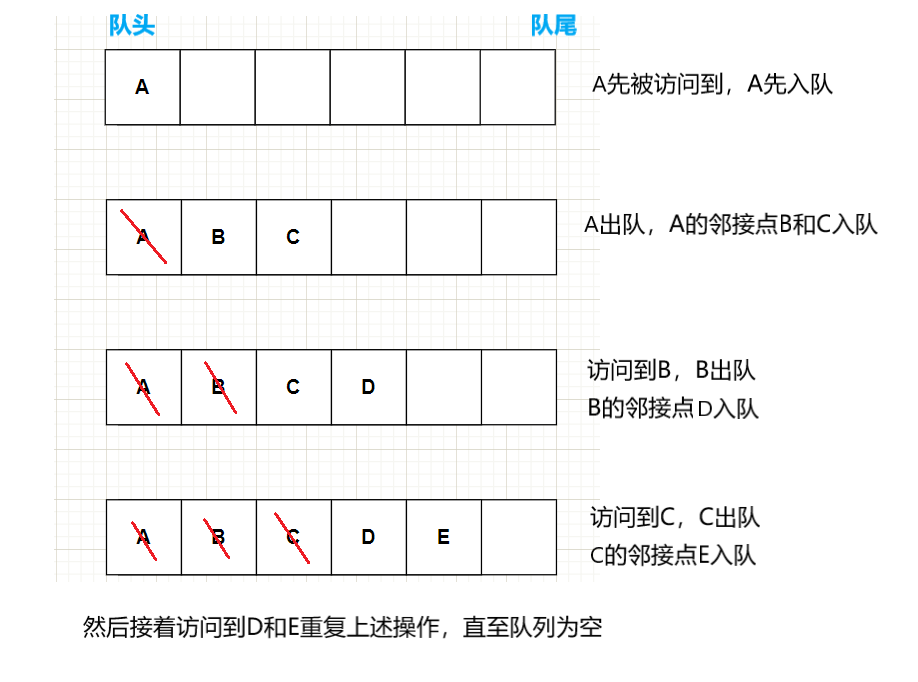
BFS的数据结构实现形式是队列，通过队列保存已被访问过的节点，利用其先进先出的特点：保证了先访问的顶点的邻接点亦先被访问

即队列保证了下图中B的邻接点比C的邻接点要先出现：

1.走迷宫（acwing 844）

给定一个 n×mn×m 的二维整数数组，用来表示一个迷宫，数组中只包含 00 或 11，其中 00 表示可以走的路，11 表示不可通过的墙壁。

最初，有一个人位于左上角 (1,1)(1,1) 处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角 (n,m)(n,m) 处，至少需要移动多少次。

数据保证 (1,1)(1,1) 处和 (n,m)(n,m) 处的数字为 00，且一定至少存在一条通路。

输入格式

第一行包含两个整数 nn 和 mm。

接下来 nn 行，每行包含 mm 个整数（00 或 11），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

1≤n,m≤1001≤n,m≤100

输入样例：

5 5

0 1 0 0 0

0 1 0 1 0

0 0 0 0 0

0 1 1 1 0

0 0 0 1 0

输出样例：

8

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

typedef pair<int, int>PII;//pair存放点的坐标

const int N = 110;

int g[N][N];//存放地图
int d[N][N];//存放点到起点的距离

// 四个方向！
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};

int n, m;

int bfs()
{
    queue<PII> q;//队列存储访问过的点以及该顶点的邻接点
    memset(d, -1, sizeof d);//初始化各个点要起点的距离为-1，表示该点没有被访问过的

    //1.起点入队
    q.push({0, 0});
    d[0][0] = 0;// 起点到自己的距离为0

    //2.while(...)
    while(q.size())
    {
        //2.1 获取队头元素 并弹出
        auto t = q.front();// 拿到队头元素
        q.pop();// 弹出队头元素

        //2.2 扩展队头元素（邻接点入队）
        for(int i = 0; i < 4; i ++)// 枚举所有邻接点
        {
            int x = t.first + dx[i];
            int y = t.second + dy[i];
            if(x >= 0 && y >= 0 && x < n && y < m && d[x][y] == -1 && g[x][y] == 0)// 判断是否满足条件
            {
                //该邻接点入队，距离增加
                q.push({x, y});
                d[x][y] = d[t.first][t.second] + 1;
            }
        }
    }

    return d[n - 1][m - 1];

}

int main()
{
    cin >> n >> m;
    //输入地图
    for (int i = 0; i < n; i ++ )
        for(int j = 0; j < m; j ++)
            cin >> g[i][j];

    cout << bfs();        

    return 0;
}

数组模拟队列：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
typedef pair<int, int> PII;
int n, m;
int g[N][N];//存放地图
int d[N][N];//存 每一个点到起点的距离
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//x 方向的向量和 y 方向的向量组成的上、右、下、左
PII q[N * N];//手写队列
int bfs()
{
    int hh = 0, tt = 0;
    q[0] = {0, 0};

    memset(d, - 1, sizeof d);//距离初始化为- 1表示没有走过

    d[0][0] = 0;//表示起点走过了

    while(hh <= tt)//队列不空
    {
        PII t = q[hh ++ ];//取队头元素

        for(int i = 0; i < 4; i ++ )//枚举4个方向
        {
            int x = t.first + dx[i], y = t.second + dy[i];//x表示沿着此方向走会走到哪个点
            if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//在边界内 并且是空地可以走 且之前没有走过
            {
                d[x][y] = d[t.first][t.second] + 1;//到起点的距离
                q[ ++ tt ] = {x, y};//新坐标入队
            }
        }
    }
    return d[n - 1][m - 1]; //输出右下角点距起点的距离即可
}
int main()
{
    cin >> n >> m;
    for(int i = 0; i < n; i ++ )
        for(int j = 0; j < m; j ++ )
            cin >> g[i][j];

    cout << bfs() << endl;

    return 0;
}

2.八数码

在一个 3×33×3 的网格中，1∼81∼8 这 88 个数字和一个 x 恰好不重不漏地分布在这 3×33×3 的网格中。

例如：

1 2 3
x 4 6
7 5 8

在游戏过程中，可以把 x 与其上、下、左、右四个方向之一的数字交换（如果存在）。

我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

1 2 3
4 5 6
7 8 x

例如，示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。

交换过程如下：

1 2 3   1 2 3   1 2 3   1 2 3
x 4 6   4 x 6   4 5 6   4 5 6
7 5 8   7 5 8   7 x 8   7 8 x

现在，给你一个初始网格，请你求出得到正确排列至少需要进行多少次交换。

输入格式

输入占一行，将 3×33×3 的初始网格描绘出来。

例如，如果初始网格如下所示：

1 2 3
x 4 6
7 5 8

则输入为：1 2 3 x 4 6 7 5 8

输出格式

输出占一行，包含一个整数，表示最少交换次数。

如果不存在解决方案，则输出 −1−1。

输入样例：

2  3  4  1  5  x  7  6  8

输出样例

19

1、题目的目标

求最小步数 -> 用BFS

2、移动情况

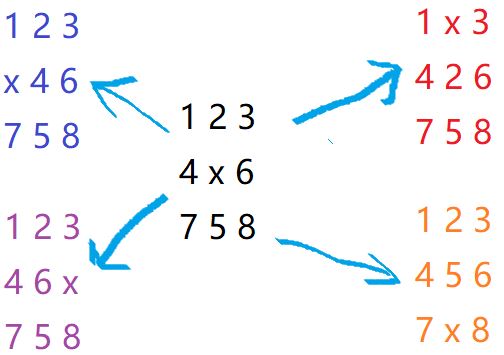
移动方式：

转以后：a = x + dx[i], b = y + dy[i].

思想：把每一个状态看作图论的一个节点（节点a到节点b的距离为1——状态能转移）——> 起点到终点最少需要多少步

从初始状况移动到目标情况 —> 求最短路

3、问题

第一点：状态如何存储到队列里？

第二点：如何记录每一个状态的“距离”（即需要移动的次数）？

第三点：队列怎么定义（队列存储的是状态，状态可以用字符串表示），dist数组怎么定义（每一个状态到起始状态的距离——两个关键字：状态(字符串)、距离(int)）——key-value？——哈希表

4、解决方案

将 “3*3矩阵” 转化为 “字符串”

如：

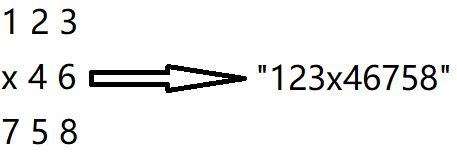
所以：

队列可以用 queue<string>
//直接存转化后的字符串
dist数组用 unordered_map<string, int>
//将字符串和数字联系在一起，字符串表示状态，数字表示距离

5、矩阵与字符串的转换方式

【参考代码】

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include<unordered_map>

using namespace std;

//状态转移
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int bfs(string strat)
{
    //定义目标状态、
    string end = "12345678x";
    //定义队列和dist数组
    queue<string> q;
    unordered_map<string, int> d;

    //初始化队列和dist数组
    q.push(strat);
    d[strat] = 0;

    while(q.size())
    {
        // 获取队头元素，弹出队列
        auto t = q.front();
        q.pop();
        //记录当前状态的距离，如果为最终状态则返回距离结果
        int distance = d[t];
        if(t == end) return d[t];

        //查询x在一位数组中的下标，进行状态转换
        int k = t.find('x');
        int x = k / 3, y = k % 3;

        //扩展队头元素（邻接节点入队）
        for(int i = 0; i < 4; i ++)
        {
            //转移后的x的坐标（邻接节点）
            int a = x + dx[i], b = y + dy[i];
            //没有越界
            if(a >= 0 && b >= 0 && a < 3 && b < 3)
            {
                //转移x
                swap(t[k], t[a * 3 + b]);
                //如果当前状态是第一次遍历，记录距离，入队
                if(!d.count(t))
                {
                    d[t] = distance + 1;
                    q.push(t);
                }
                //还原状态，为下一种转换情况做准备！
                swap(t[k], t[a * 3 + b]);
            }
        }
    }

    //无法转换到目标状态，返回-1
    return -1;

}

int main()
{

    string strat;
    // 输入起始状态
    for (int i = 0; i < 9; i ++ )
    {
        char c;
        cin >> c;
        strat += c;
    }

    cout << bfs(strat);

}

总结常用技巧：一维数组与二维数组坐标的转换

设[一维数组]下标为index（从0开始），二维数组长度为m * n，则：

一维数组转换为二维数组

x = index / n
y = index % n

二维数组转换为一维数组

index = x + y * n

学习内容部分转载自：

1.​ acwing算法基础课

2.作者：四谷夕雨

链接：https://www.acwing.com/solution/content/15149/

注：如果文章有任何错误或不足，请各位大佬尽情指出，评论留言留下您宝贵的建议！如果这篇文章对你有些许帮助，希望可爱亲切的您点个赞推荐一手，非常感谢啦