【2.0 递归 Recursion 01】

【介绍】

Java的一个方法可以调用它自己，Java和所有编程语言都可以支持这种情况，我们把它叫做递归Recursion

递归方法是一种调用自身的方法

那么使用递归方法是是怎么样的呢，让我们看看下面这段代码

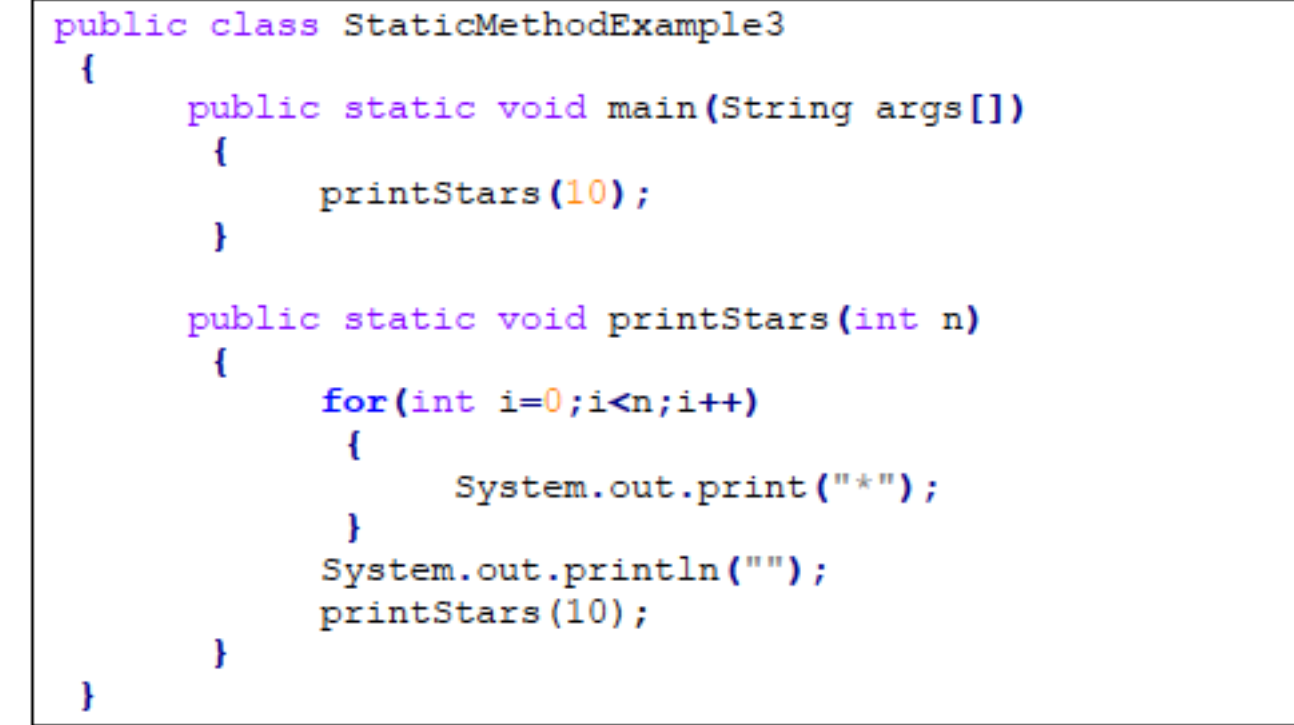
（由于复制粘贴代码还要考虑排版，这里就上图了）

结果是程序会一直在调用这个方法，直到内存不足而停止（无限套娃）

【概念】

方法反复调用自身的概念称为递归

方法会不断调用自身，直到达到某些停止条件为止，有点像循环语句

在没有停止条件的情况下，程序将循环运行，直到计算机（Java虚拟机）内存不足（拒绝分配更多的内存）为止

虽然递归可能显得浪费甚至效率低下，但它在计算机科学和数学中是一个非常重要的概念

递归更像是一种思想，我们需要打破原有的“迭代”的思维定势（for,while）

为了帮助可视化“递归”，我们将使用一个称为堆栈 Stack的通用概念

堆栈基本上像自助餐厅中的托盘容器一样工作。它只有两个操作：

Push:你可以把某个东西压到栈上

Pop:你可以从堆栈的顶部弹出一些东西

First In Last Off

通过下面这张图感受一下

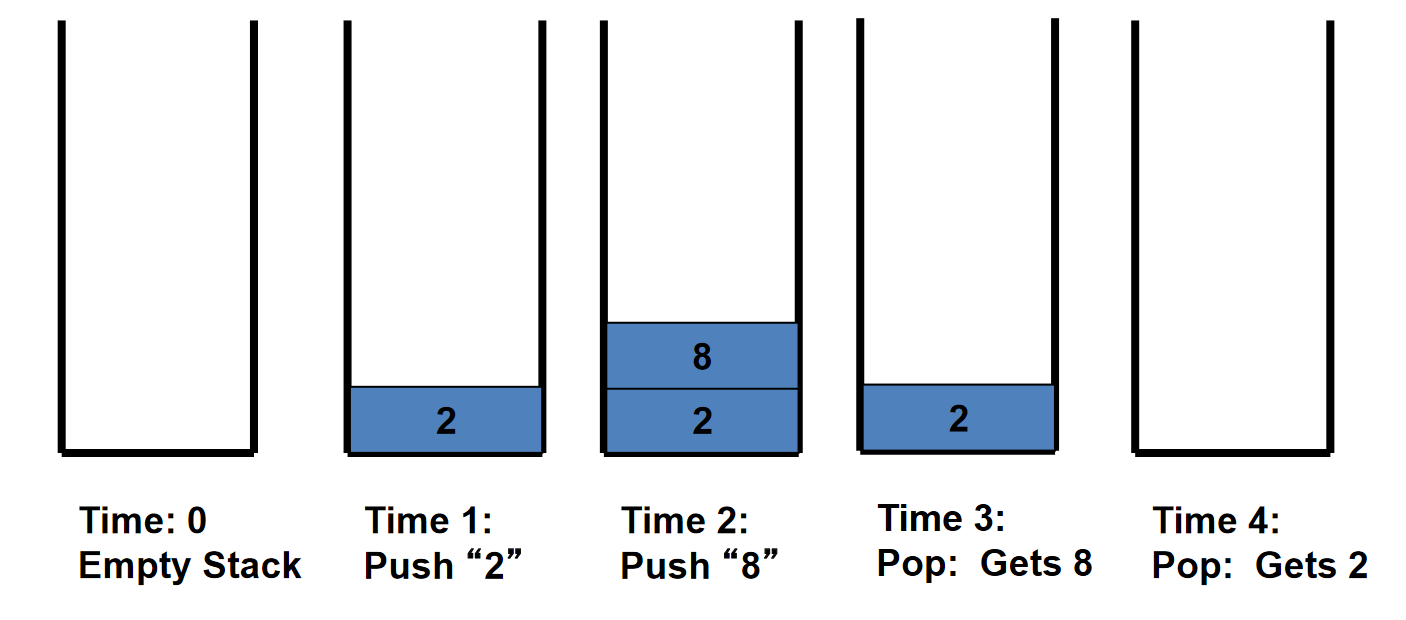
有的人说这就像弹匣一样，拉出来装Push然后从第一发开始射击Pop

【堆栈和方法 Stacks and Methods】

当你运行一个程序时，计算机会为你创建一个堆栈

每次调用方法时，该方法都会放在堆栈的顶部

当方法返回或退出时，该方法将从堆栈中弹出

【堆栈和递归 Stacks and Recursion】

每次调用方法时，都将该方法推入堆栈

每次方法返回或退出时，都将方法弹出堆栈

如果一个方法递归地调用自己，您只需将该方法的另一个副本压入堆栈

对于下面的这个简单程序：

public class Recursion1V0{
public static void main (String args[]) {
      count(0);
      System.out.println();
}
public static void count (int index) {
      System.out.print(index);
      if (index < 2) count(index+1);
}
}

我们将这个过程可视化之后便是这样

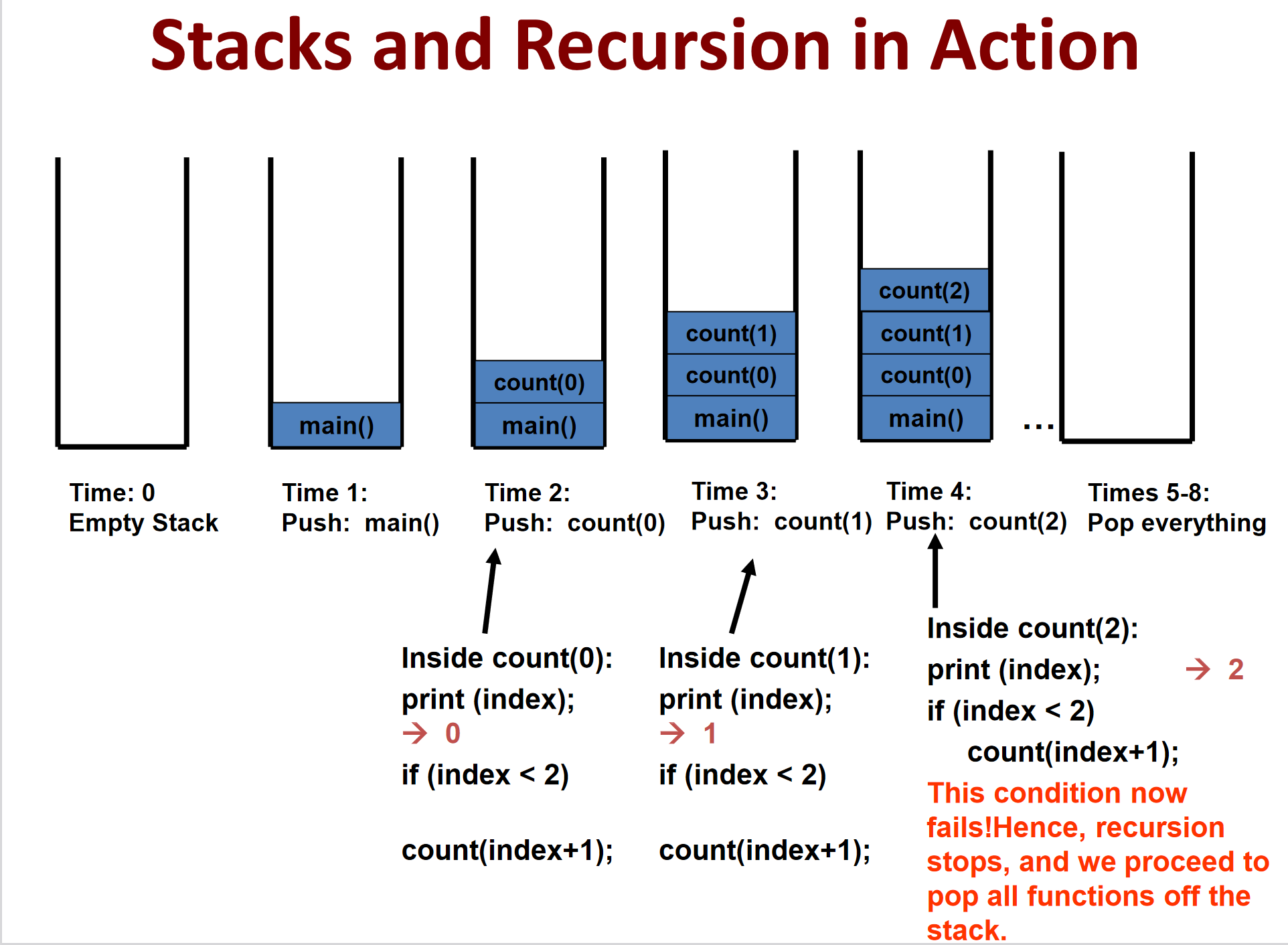
如果我们把代码改成

public class Recursion1V0{
public static void main (String args[]) {
      count(0);
      System.out.println();
}
public static void count (int index) {

      if (index < 2) count(index+1);
      System.out.print(index);  //注意这里！
}
}

此时的输出是2 1 0 为什么呢，我们回忆一下堆栈的Push和Pop，就知道为什么了（FirstIn,LastOff）

我们需要一个方法执行结束（return好了），再执行接下来的操作

count(0)到count(1)到count(2)，结束执行，随后执行System.out.print(index)，分别打印210

【两种类型的递归】

1.直接递归 Direct recursion

方法直接包含对自身的引用或调用

2.间接递归 Indirect Recursion

一个方法调用另一个方法，该方法最终调用原始方法（比如A方法调用B方法，B方法调用A方法）

递归计算通过使用相同问题的解决方案来解决问题，但是具有更简单的值。我们称此为递归步骤 recursive step

为了使递归终止或停止，还必须有最简单值的特殊情况,我们称之为基本情况base case/anchor case/stopping condition

基本情况是为输入参数的一个或多个已知值指定方法值的情况

递归步骤(或归纳步骤)是根据先前定义的值定义对参数的当前值所采取的操作

为了执行递归，我们必须考虑以下两个方面

1.如何解决最简单的问题

2.给定一个更复杂的问题实例，如何使其更像最简单的实例？即如何使它更接近问题的最简单实例（使其像基本情况一样）？

【三步使用递归 Three Steps to Recursive Success 】

动手试试，我们写一个程序来检测字符串是否是回文（比如NAVAN）

1.减少 Reduction ——使问题变小

可以直接检测首尾的字符，如果它们是相同的，那么我们就删除它们（如果一开始就是回文如NAVAN，那么删除后得到的部分也是回文AVA）

2.基本情况 Base Cases ——处理简单的值，关键是找到最简单的情况的解决方案

比如有下面几个情况

1.最后没有字符了——是回文

2.最后剩下一个字符——是回文

3.最后剩下两个字符且二者不是同一个字符——不是回文

3.执行 Implement ——结合基本情况与步骤