C++一元多项式求导

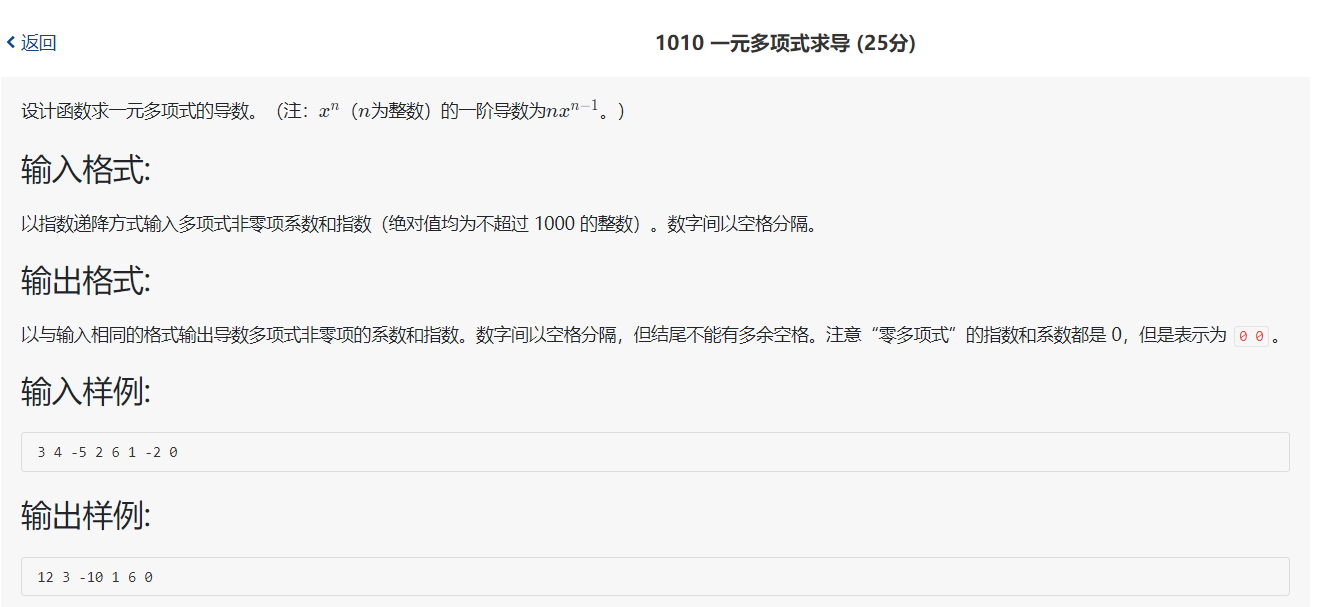
这个题难度不大但是坑有点多，要考虑的点有几个：

1.测试用例为x 0 这个直接输出 0 0即可。

2.注意空格的输出

3.测试点3我好几次都没过，最后参考了别的答案加以修改才通过。

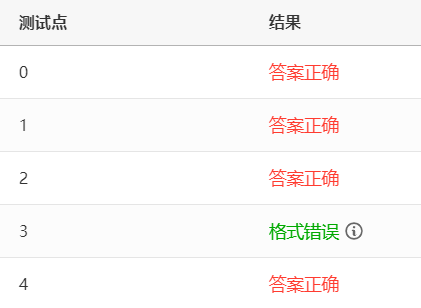
测试点3没过的代码：

 1 #include <iostream>
 2 #include <vector>
 3
 4 using namespace std;
 5
 6 struct Derivative
 7 {
 8     int ratios;//系数
 9     int time;//次数
10 };
11
12 int main()
13 {
14     int ratios;
15     int time;
16
17     //接收输入
18     vector<Derivative> derivatives;
19     while(cin >> ratios >> time)
20     {
21         Derivative d;
22         d.ratios = ratios;
23         d.time = time;
24         derivatives.push_back(d);
25         char c = cin.get();
26         if(c == '\n')
27             break;
28     }
29
30     for(vector<Derivative>::iterator it = derivatives.begin();it != derivatives.end();++it)
31     {
32          if((*it).time != 0)
33         {
34             (*it).ratios *= (*it).time;
35             (*it).time--;
36             cout << (*it).ratios << " " << (*it).time;
37             if((*it).time != 0 && it != derivatives.end()-1)
38                 cout << " ";
39         }
40         if(it == derivatives.begin() && (*it).time == 0)
41         {
42             cout << "0 0";
43         }
44     }
45     return 0;
46 }

只有在每组结束后输出空格的代码不同。

最终的代码：

 1 #include <iostream>
 2 #include <vector>
 3
 4 using namespace std;
 5
 6 struct Derivative
 7 {
 8     int ratios;//系数
 9     int time;//次数
10 };
11
12 int main()
13 {
14     int ratios;
15     int time;
16
17     //接收输入
18     vector<Derivative> derivatives;
19     while(cin >> ratios >> time)
20     {
21         Derivative d;
22         d.ratios = ratios;
23         d.time = time;
24         derivatives.push_back(d);
25         char c = cin.get();
26         if(c == '\n')
27             break;
28     }
29
30     for(vector<Derivative>::iterator it = derivatives.begin();it != derivatives.end();++it)
31     {
32         //次数不为0时，就输出经过处理的系数和指数
33         if((*it).time != 0)
34         {
35             if(it != derivatives.end() && it != derivatives.begin())
36                 cout << " ";
37             (*it).ratios *= (*it).time;
38             (*it).time--;
39             cout << (*it).ratios << " " << (*it).time;
40         }else if((*it).time == 0 && it == derivatives.begin())
41         {
42             //第一项的次数就为0时，直接输出0 0
43             cout << "0 0";
44         }
45     }
46
47
48     return 0;
49
50 }