八皇后问题-dfs

一、题意解析

　　国际象棋中的皇后，可以横向、纵向、斜向移动。如何在一个8X8的棋盘上放置8个皇后，使得任意两个皇后都不在同一条横线、竖线、斜线方向上？八皇后问题是一个古老的问题，于1848年由一位国际象棋棋手提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，如何求解？以高斯为代表的许多数学家先后研究过这个问题。后来，当计算机问世，通过计算机程序的运算可以轻松解出这个问题。

二、如何解决八皇后问题？

　　所谓递归回溯，本质上是一种枚举法。这种方法从棋盘的第一行开始尝试摆放第一个皇后，摆放成功后，递归一层，再遵循规则在棋盘第二行来摆放第二个皇后。如果当前位置无法摆放，则向右移动一格再次尝试，如果摆放成功，则继续递归一层，摆放第三个皇后......

　　如果某一层看遍了所有格子，都无法成功摆放，则回溯到上一个皇后，让上一个皇后右移一格，再进行递归。如果八个皇后都摆放完毕且符合规则，那么就得到了其中一种正确的解法。说起来有些抽象，我们来看一看递归回溯的详细过程。

　　1.第一层递归，尝试在第一行摆放第一个皇后：

　　2.第二层递归，尝试在第二行摆放第二个皇后（前两格被第一个皇后封锁，只能落在第三格）：

　　3.第三层递归，尝试在第三行摆放第三个皇后（前四格被第一第二个皇后封锁，只能落在第五格）：

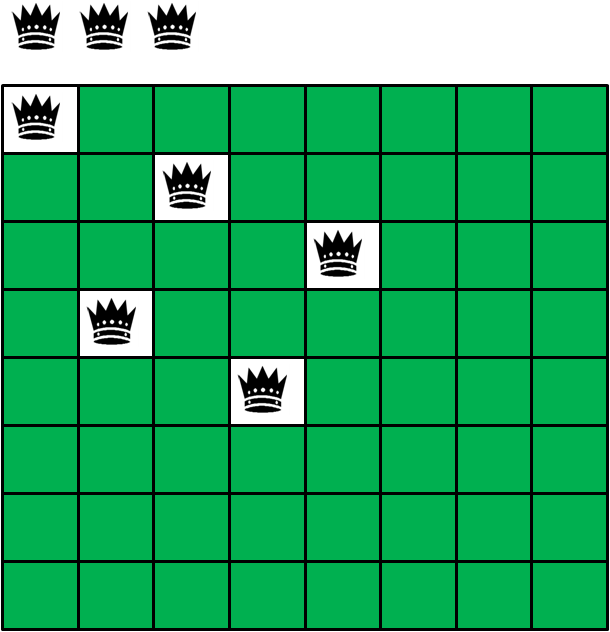
　　4.第四层递归，尝试在第四行摆放第四个皇后（第一格被第二个皇后封锁，只能落在第二格）：

　　5.第五层递归，尝试在第五行摆放第五个皇后（前三格被前面的皇后封锁，只能落在第四格）：

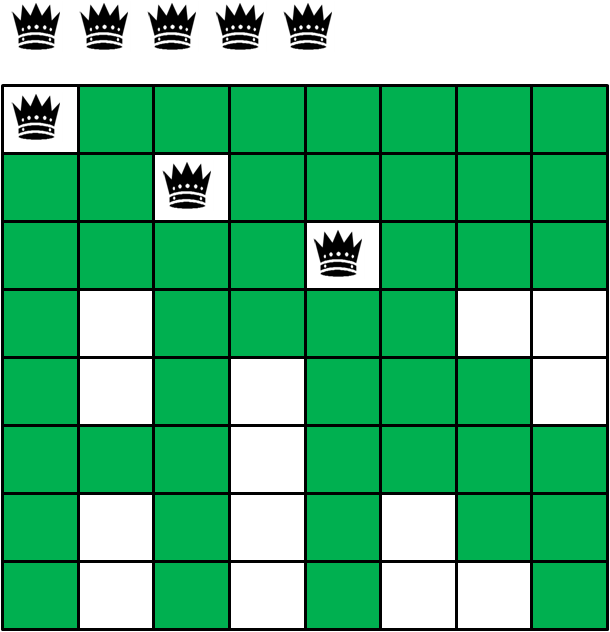
　　6.由于所有格子都“绿了”，第六行已经没办法摆放皇后，于是进行回溯，重新摆放第五个皇后到第八格。：

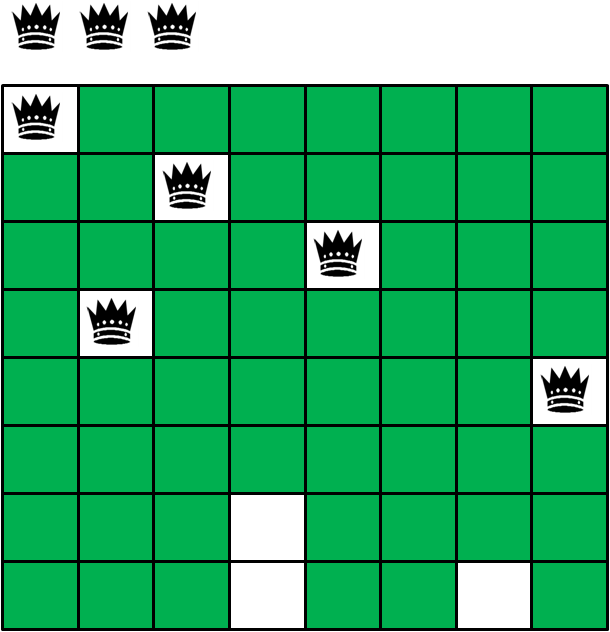
　　7.第六行仍然没有办法摆放皇后，第五行也已经尝试遍了，于是回溯到第四行，重新摆放第四个皇后到第七格。：

　　8.继续摆放第五个皇后，以此类推......

代码：打印所有的摆放方法以及方法总数

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<string>
#include<sstream>
#include<iostream>
using namespace std;

int num=;

void output(bool arr[][])
{
    num++;
    printf("\n");
    for(int i=;i<;i++)
    {
        for(int j=;j<;j++)
            printf("%d ",arr[i][j]);
        printf("\n");
    }
}

bool check(bool arr[][],int row,int column)///检查落子是否合法，参数分别是行，列
{
    if(row==)  ///第一行落子肯定合法
        return true;

    ///一行只摆一个就换行，所以不用判断行是否合法

    int i,j;///判断同一列上有没有棋子
    for(i=;i<row;i++)
    {
        if(arr[i][column])
            return false;
    }
    i=row-;
    j=column-;///判断左上斜线是否有棋子
    while(i>=&&j>=)
    {
        if( arr[i][j] )
        {
            return false;
        }
        i--;
        j--;
    }
    i=row-;
    j=column+;///判断右上斜线是否有棋子
    while(i>=&&j<)
    {
        if( arr[i][j] )
        {
            return false;
        }
        i--;
        j++;
    }
    return true;
}

void slove(bool arr[][],int row)///回溯法，核心代码
{///从第一行第一列开始摆放，如果合法就继续摆，深度搜索所有答案
    for(int column=;column<;column++)
    {
        arr[row][column]=true;///摆下去先，再判断是否落子合法
        if( check(arr,row,column) )
        {
            if( row+== )  ///摆到第八行，并且落子合法，则棋盘正确摆放了
                output(arr);
            else
                slove(arr,row+);///如果该落子合法，又没有到第八行，则继续下一行开摆
        }
        arr[row][column]=false;///不摆这一颗子，摆下一颗子进行深度搜索
    }
}
int main()
{
    bool chess[][];
    memset(chess,false,sizeof(chess));
    slove(chess,);
    printf("num=%d\n",num);
    return ;
}