[jzoj]3777.最短路（shortest）

Link

　　https://jzoj.net/senior/#main/show/3777

Description

　　小Y最近学得了最短路算法，一直想找个机会好好练习一下。话虽这么说，OJ上最短路的题目都被他刷光了。正巧他的好朋友小A正在研究一类奇怪的图，他也想凑上去求下它的最短路。
       小A研究的图可以这么看：在一个二维平面上有任意点(x,y)（0<=x<=N,0<=y<=M,且x,y均为整数），且(x,y)向(x-1,y)（必须满足1<=x）和(x,y-1)（必须满足1<=y）连一条边权为0的双向边。
       每个点都有一个非负点权，不妨设(x,y)的权值为F[x][y]，则有：
       1.x=0或y=0：F[x][y]=1；2.其他情况：F[x][y]=F[x-1][y]+F[x][y-1]。
       现在，小Y想知道(0,0)到(N,M)的最短路，即使得经过的点的权值之和最小。为了炫耀自己学过最短路算法，他决定和你进行一场比赛，看谁的程序跑得快。然则小Y没有学过高精度算法，所以他希望输出答案时只输出答案模1000000007后的值。

Solution

题目大意

　　求从(0,0)~(n,m)经过点的和的最小值。

　　第(x,y)点的权值为f[x,y]，他的计算方法是f[x,y]=f[x-1,y]+f[x,y-1]，如果(x=0) or (y=0)那么f[x,y]的值为1

60分

　　很显然，可以直接暴力枚举，求出答案。

100分

　　通过一系列的对拍，我们可以发现，如下图红边的走法，必定最优，但不知道怎么证明。我们设较短边的长为n，较长边的长为m

　　

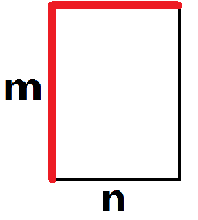
　　我们可以总结成一个公式

　　

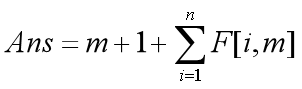
　　那么，关键就成了如何求出F[i,m] (i=1~n)。

　　我们考虑把他转化成组合数的形式

　　根据题目给出的F数组计算方法，可以得出f[x,y]=C(min(x,y),x+y)

　　那么显然F[i,m] (i=1~n)就是C(i,i+m) (i=1~n)

　　其实每个组合数，可以理解成一个数除另一个数，比如对于C(n,m)

　　

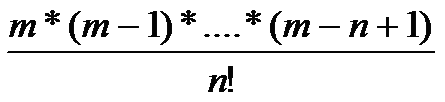
　　试想一下，如果x<y，求C(x,y)+C(x+1,y+1)+C(x+2,y+2)，我们设上面这个式子分子为tot1，分母为tot2

　　C(x+1,y+1)相比C(x,y)的tot1和tot2，发现tot1多乘了y+1，tot2多乘了x+1，

　　C(x+2,y+2)相比C(x+1,y+1)的tot1和tot2，发现tot1多乘了y+2，tot2多乘了x+2

　　说明，我们每次循环，tot1都乘i+m，tot2都乘i，那么，每次的C(i,i+m)就是tot1/tot2

　　但是问题来了,tot1和tot2都很大，如果相除是不太可能的，先mod再除答案是错误的，只能使用逆元了。

逆元

　　根据费马小定理可以得到如下式子

　　

　　两边同时除b得到，高斯研究过，发现是等价的

　　

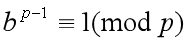
　　 两边同时除b得到，高斯研究过，发现是等价的

　　

　　两边同时乘一个a，并且交换位置，得到如下式子

　　

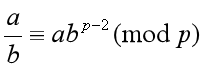
　　发现，我们要求a除b取模p的结果，其实是等价于ab^p-2取模p的结果的，也就是说，欲想知道a除b取模p的结果，其实就是算出ab^p-2取模p的结果就行了

　　因为a*b mod p，是等价于a mod p*b mod p的，a^k mod p是等价于(a mod p)^k的，所以我们这里可以取mod来避免高精度。

　　当然，F[i,m] (i=1~n)这一部分，可以使用一个组合公式就可以了，具体实现和题解请选手自行考虑。