APIO2013 tasksauthor

喜闻乐见的提答题，这道题还是蛮有趣的

数据结构题写得心塞，来一道提答意思意思

如果喜欢这类题的话还可以去做做uoj83。

这题是给出了两个问题，一个最短路，一个无向图染色问题。

Data 1

Floyd VS Dijkstra

嗯107个整数，我们只要给一个n=101，下面一坨0 Floyd就狗带了

#include <iostream>
#include <stdio.h>
using namespace std;
int main()
{
    printf("101\n");
    for(int i=;i<=;i++) puts("");
    puts("");
    printf("%d %d\n",,);
}

Data 2

啥Floyd 艹 Bellman-Ford？

看了一下代码…似乎真的可以随便艹掉。

Floyd：O(n^3)，询问O(1)。

Bellman-Ford：询问O(ne)。

似乎随机数据一波就行？然而随机数据烂了。

这个点就是想让我们得到一个让bellman-ford和理论复杂度相差无几的数据。

其实很简单啊…加一坨没用的自环，然后剩下的搞一个5->4->3->2->1这样的链即可。

#include <iostream>
#include <stdio.h>
using namespace std;
int main()
{
    puts(""); int mm=;
    for(int i=;i<;i++)
    {
        int mx=min(mm,),mxx=mx; mm-=mx;
        if(i!=) ++mx;
        printf("%d",mx);
        if(i!=) printf(" %d 2333",i-);
        for(int j=;j<=mxx;j++) printf(" %d 2333",i);
        putchar();
    }
    puts("");
    for(int i=;i<=;i++) printf("99 0\n");
}

Data 3

Bellman-Ford vs Floyd

用data 1即可

Data 4

Floyd 艹 Dijkstra！限制157个数！

咦似乎文件名叫“ModifiedDijkstra”看起来非常厉害

看了一下代码似乎没什么问题

咦可以有负权边…

怎么搞呢？如图所示。

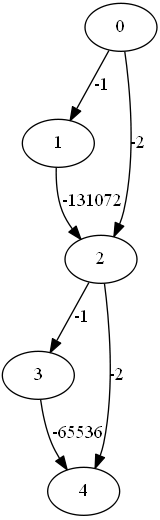
这里的更新顺序会变成0,2,4,3,4,1,2,4,3,4，这样再接上去几个就成了指数级啦

#include <iostream>
#include <stdio.h>
using namespace std;
int main()
{
    int bs=*(<<),n=; //可能要调一下
    printf("%d\n",n);
    for(int i=;i<n;i++)
    {
        if(i==n-) {puts(""); continue;}
        else if(i&) printf("1 %d %d\n",i+,-(bs/=));
        else printf("2 %d %d %d %d\n",i+,-,i+,-);
    }
    puts("");
    for(int i=;i<=;i++) printf("0 %d\n",n-);
}

UPD：这道题的改进版出现在IPSC2015 D，大家可以试做一下。

Data 5

Dijkstra 艹 Bellman-Ford

需要把Data 2稍加优化（人肉二分）

#include <iostream>
#include <stdio.h>
using namespace std;
int main()
{
    int N=; int cnt=;
    printf("%d\n",N), cnt++; int mm=;
    for(int i=;i<N;i++)
    {
        int mx=min(mm,),mxx=mx; mm-=mx;
        if(i!=) ++mx;
        printf("%d",mx), cnt++;
        if(i!=) printf(" %d 2333",i-), cnt+=;
        for(int j=;j<=mxx;j++) printf(" %d 2333",i), cnt+=;
        putchar();
    }
    puts(""), ++cnt;
    for(int i=;i<=;i++) printf("%d 0\n",N-), cnt+=;
    cerr<<"cnt="<<cnt<<"\n";
}

Data 6

Bellman-Ford 艹 Dijkstra

用Data 4即可。

Data 7

这回是一个平面图染色问题。

我们发现Gamble1是不会T的，现在我们就要让RecursiveBacktracking T掉。

我随机生成了个树，随机加了一坨边，就T了。

#include <iostream>
#include <stdio.h>
#include <map>
using namespace std;
map<int,bool> ms[];
int main()
{
    int n=,m=;
    printf("%d %d\n",n,m);
    for(int i=;i<n;i++)
    {
        int p=rand()%i;
        printf("%d %d\n",i,p), --m;
        ms[i][p]=ms[p][i];
    }
    while(m)
    {
        int a=rand()%n,b=rand()%n;
        if(ms[a][b]||a==b) continue;
        printf("%d %d\n",a,b);
        ms[a][b]=ms[b][a]=;
        --m;
    }
}

Data 8

要让RecursiveBacktracking A掉而且数据范围有下限

随便搞啦

这份代码生成粗来类似这样

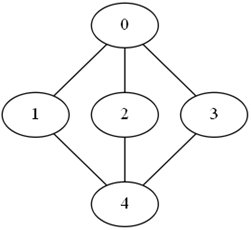
随手加了一点重边什么的

#include <iostream>
#include <stdio.h>
#include <map>
using namespace std;
map<int,bool> ms[];
#define BS 4
int main()
{
    int n=/BS*BS+,m=;
    printf("%d %d\n",n,m);
    for(;;)
    {
    for(int i=;i<n;i++)
    {
        if(i==n-) continue;
        if(i%BS==)
        {
            for(int j=;j<BS;j++)
            {
                --m;
                printf("%d %d\n",i,i+j);
                if(!m) exit();
            }
        }
        else
        {
            --m;
            printf("%d %d\n",i,(i/BS+)*BS);
            if(!m) exit();
        }
    }
    }
}

感觉这道题答出的还行，大概做了2h的样子