【Codeforces-707D】Persistent Bookcase DFS + 线段树

D. Persistent Bookcase

Recently in school Alina has learned what are the persistent data structures: they are data structures that always preserves the previous version of itself and access to it when it is modified.

After reaching home Alina decided to invent her own persistent data structure. Inventing didn't take long: there is a bookcase right behind her bed. Alina thinks that the bookcase is a good choice for a persistent data structure. Initially the bookcase is empty, thus there is no book at any position at any shelf.

The bookcase consists of n shelves, and each shelf has exactly m positions for books at it. Alina enumerates shelves by integers from 1to n and positions at shelves — from 1 to m. Initially the bookcase is empty, thus there is no book at any position at any shelf in it.

Alina wrote down q operations, which will be consecutively applied to the bookcase. Each of the operations has one of four types:

• 1 i j — Place a book at position j at shelf i if there is no book at it.
• 2 i j — Remove the book from position j at shelf i if there is a book at it.
• 3 i — Invert book placing at shelf i. This means that from every position at shelf i which has a book at it, the book should be removed, and at every position at shelf i which has not book at it, a book should be placed.
• 4 k — Return the books in the bookcase in a state they were after applying k-th operation. In particular, k = 0 means that the bookcase should be in initial state, thus every book in the bookcase should be removed from its position.

After applying each of operation Alina is interested in the number of books in the bookcase. Alina got 'A' in the school and had no problem finding this values. Will you do so?

Input

The first line of the input contains three integers n, m and q (1 ≤ n, m ≤ 103, 1 ≤ q ≤ 105) — the bookcase dimensions and the number of operations respectively.

The next q lines describes operations in chronological order — i-th of them describes i-th operation in one of the four formats described in the statement.

It is guaranteed that shelf indices and position indices are correct, and in each of fourth-type operation the number k corresponds to some operation before it or equals to 0.

Output

For each operation, print the number of books in the bookcase after applying it in a separate line. The answers should be printed in chronological order.

Examples

input

2 3 3
1 1 1
3 2
4 0

output

1
4
0

input

4 2 6
3 2
2 2 2
3 3
3 2
2 2 2
3 2

output

2
1
3
3
2
4

input

2 2 2
3 2
2 2 1

output

2
1

Note

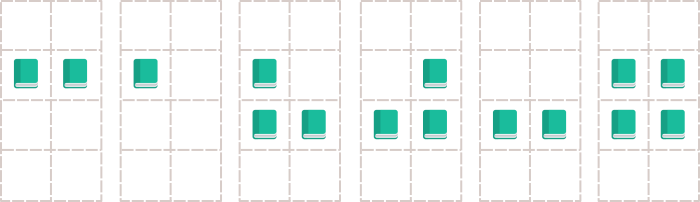
This image illustrates the second sample case.

Solution

 题目大意：

给出一个矩阵，要支持如下操作

1.（x，y）位置变成1

2.（x，y）位置变成0

3.整行取反，0变成1，1变成0

4.退回到第k次操作后的状态

一共Q次询问，每次询问后输出矩阵中1的个数

首先，把矩阵展成序列，对其建线段树，这样，1，2，3操作就是简单的单点修改，区间修改

操作4的难处在于空间不允许保存历史状态，

考虑离线。

首先假设我们得到$i$之前的所有操作的答案，$i+1$次操作是退回操作，显然$i+1$次操作的答案，可以通过以前的答案得到，但问题涉及状态的变化

很显然，一次退回操作就相当于将这个操作之后的，到下一次退回操作之前的所有操作，从其退回到的状态开始修改

这显然是个树形的结构，于是我们的方法就非常直观了

对于所有的操作，我们假定$i$操作是向$i+1$操作连一条单向边的，那么对于一个退回操作$k$，它所退回到的操作是$x$,就相当于从$x$也向$k+1$连一条单向边，然后我们用$x$把$k$的答案更新，去掉$k$既可

那么从一号操作为根的树上DFS，每次修改，记录答案，修改完后回溯，直到遍历整棵树

而这样，状态不能记录的问题就被解决了，只需要一棵线段树，不过是修改2Q次

一个操作，可能不合法，这时候需要记录一下，回溯的时候特判

Code

code from yveh

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
struct edgetype{
    int s,t,next;
}e[];
int head[],cnt=;
void addedge(int s,int t)
{
    e[cnt].s=s;e[cnt].t=t;e[cnt].next=head[s];head[s]=cnt++;
}
struct Node{
    int data,size;
    bool rev;
    Node()
    {
        data=rev=;
    }
};
bool flag;
namespace Segtree
{
    Node tree[];
    void pushup(int node)
    {
        tree[node].data=tree[node<<].data+tree[node<<|].data;
    }
    void build(int l,int r,int node)
    {
        tree[node].size=r-l+;
        if (l==r)
            return;
        int mid=(l+r)>>;
        build(l,mid,node<<);
        build(mid+,r,node<<|);
    }
    void pushdown(int node)
    {
        if (tree[node].rev)
        {
            tree[node<<].data=tree[node<<].size-tree[node<<].data;
            tree[node<<].rev^=;
            tree[node<<|].data=tree[node<<|].size-tree[node<<|].data;
            tree[node<<|].rev^=;
            tree[node].rev=;
        }
    }
    void modify_pos(int pos,int l,int r,int node,int val)
    {
        if (l==r)
        {
            flag=tree[node].data==val;
            tree[node].data=val;
            return;
        }
        pushdown(node);
        int mid=(l+r)>>;
        if (pos<=mid)
            modify_pos(pos,l,mid,node<<,val);
        else
            modify_pos(pos,mid+,r,node<<|,val);
        pushup(node);
    }
    void modify_rev(int L,int R,int l,int r,int node)
    {
        if (L<=l&&r<=R)
        {
            tree[node].data=tree[node].size-tree[node].data;
            tree[node].rev^=;
            return;
        }
        pushdown(node);
        int mid=(l+r)>>;
        if (L<=mid)
            modify_rev(L,R,l,mid,node<<);
        if (R>mid)
            modify_rev(L,R,mid+,r,node<<|);
        pushup(node);
    }
    int query()
    {
        return tree[].data;
    }
}
int n,m,q,opt,u,v,k;
int a[][],ans[];
void init()
{
    scanf("%d%d%d",&n,&m,&q);
    Segtree::build(,n*m,);
}
void dfs(int node)
{
    if (a[node][]==)
    {
        Segtree::modify_pos((a[node][]-)*m+a[node][],,n*m,,a[node][]);
        if (!flag)
            a[node][]=;
        else
            a[node][]=;
    }
    if (a[node][]==)
    {
        Segtree::modify_pos((a[node][]-)*m+a[node][],,n*m,,a[node][]);
        if (!flag)
            a[node][]=;
        else
            a[node][]=;
    }
    if (a[node][]==)
        Segtree::modify_rev((a[node][]-)*m+,a[node][]*m,,n*m,);
    ans[node]=Segtree::query();
    for (int i=head[node];i!=-;i=e[i].next)
        dfs(e[i].t);
    if (a[node][]==)
        Segtree::modify_pos((a[node][]-)*m+a[node][],,n*m,,a[node][]);
    if (a[node][]==)
        Segtree::modify_pos((a[node][]-)*m+a[node][],,n*m,,a[node][]);
    if (a[node][]==)
        Segtree::modify_rev((a[node][]-)*m+,a[node][]*m,,n*m,);
}
void work()
{
    memset(head,0xff,sizeof(head));
    cnt=;
    for (int i=;i<=q;i++)
    {
        scanf("%d",&a[i][]);
        if (a[i][]==)
        {
            scanf("%d%d",&a[i][],&a[i][]);
            a[i][]=;
        }
        if (a[i][]==)
        {
            scanf("%d%d",&a[i][],&a[i][]);
            a[i][]=;
        }

        if (a[i][]==)
            scanf("%d",&a[i][]);
        if (a[i][]==)
        {
            scanf("%d",&k);
            addedge(k,i);
        }
        else
            addedge(i-,i);
    }
    dfs();
    for (int i=;i<=q;i++)
        printf("%d\n",ans[i]);
}
int main()
{
    init();
    work();
    return ;
}

YveH打CF时问我的题...当时蹦出这个想法，但是他没能来得及当场A掉

觉得思路挺有意义的一道题，所以留下了想法...

实际上我还不知道题解是什么.....