以Top-Down思维去解决问题——递归

目录

• 递归的基础
• 递归的底层实现（不是重点）
• 递归的应用场景
• 编程中 两种解决问题的思维
  • 自下而上（Bottom-Up）
  • 自上而下（Top-Down）
• 自上而下的思考过程——求和案例
• 台阶问题 案例
• 易位构词生成 案例

---

递归和for循环（迭代法）很像，都是通过循环去完成一件事。

但采用Top-Down思维去设计的递归结构，又会比for多一些不同的能力。多什么能力？

递归的基础

先复习一下递归，递归的定义：递归（英语：Recursion），又译为递回，在数学与计算机科学中，是指在函数的定义中使用函数自身的方法。

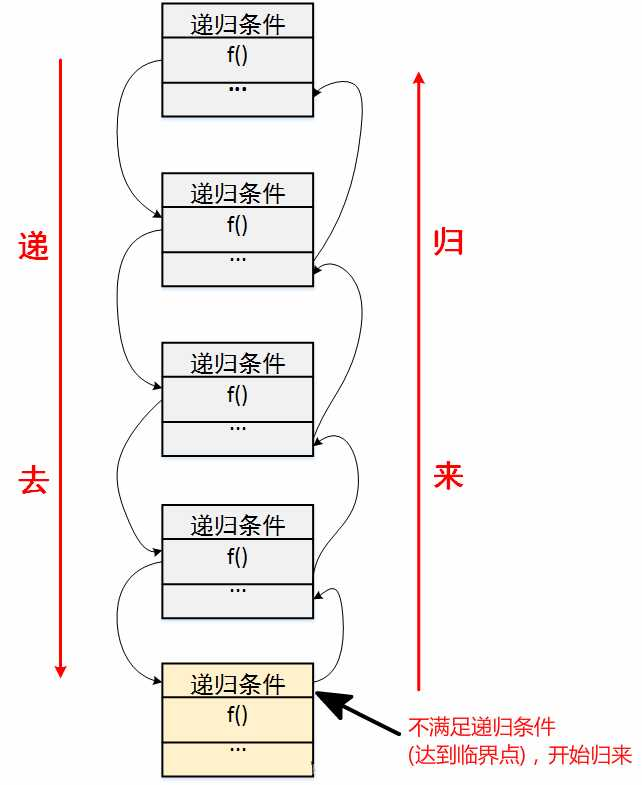
递归的本质就在：递去，归来 两个流程中。 初学者刚接触会有点抽象，下面通过一些案例来认识。

假设需要你实现一个阶乘的计算函数，

阶乘的定义：

5的阶乘是 5*4*3*2*1=120

def factorial(number):
    if number == 1:
        return 1
    else:
        return number * factorial(number - 1)

print(factorial(5))
// 120

递归需要考虑三个条件：

1. 将问题拆分成一个重复使用的子问题；
2. 注意，这个子问题和问题的规模无关；
3. 必须包含终止条件 (终止条件即初始状态)。

递归的底层实现（不是重点）

递归的底层实现不是本文的重点，了解一下就行。

递归在编程语言的底层实现通常依赖于调用栈（call stack）：

• 调用栈：

  • 每次函数调用时，程序会将函数的参数、局部变量和返回地址等信息压入栈帧。
  • 当递归函数调用自身时，会创建新的栈帧压入栈中。
  • 函数执行完毕后，栈帧被弹出，返回控制权给调用者。

• 基线条件：

  • 递归必须有终止条件，否则会导致栈溢出（stack overflow）。
  • 每次递归调用都应该向基线条件靠近。

• 内存管理：

  • 调用栈通常在内存的“栈区”分配。栈的大小有限制，过多的递归调用可能导致栈溢出。
  • 有些语言提供机制来增加栈的大小，但一般不推荐依赖深层递归。

总结：

• 递归实现的效率和安全性与具体语言的特性和编译器的优化密切相关。

• 递归的底层实现，就是把相关变量数据（缓存）处理后，一层一层的压入栈，等到了基准条件后，在逐层拿出处理。

计算机眼里的递归：

计算机使用栈来记录正在调用的函数，叫调用栈。

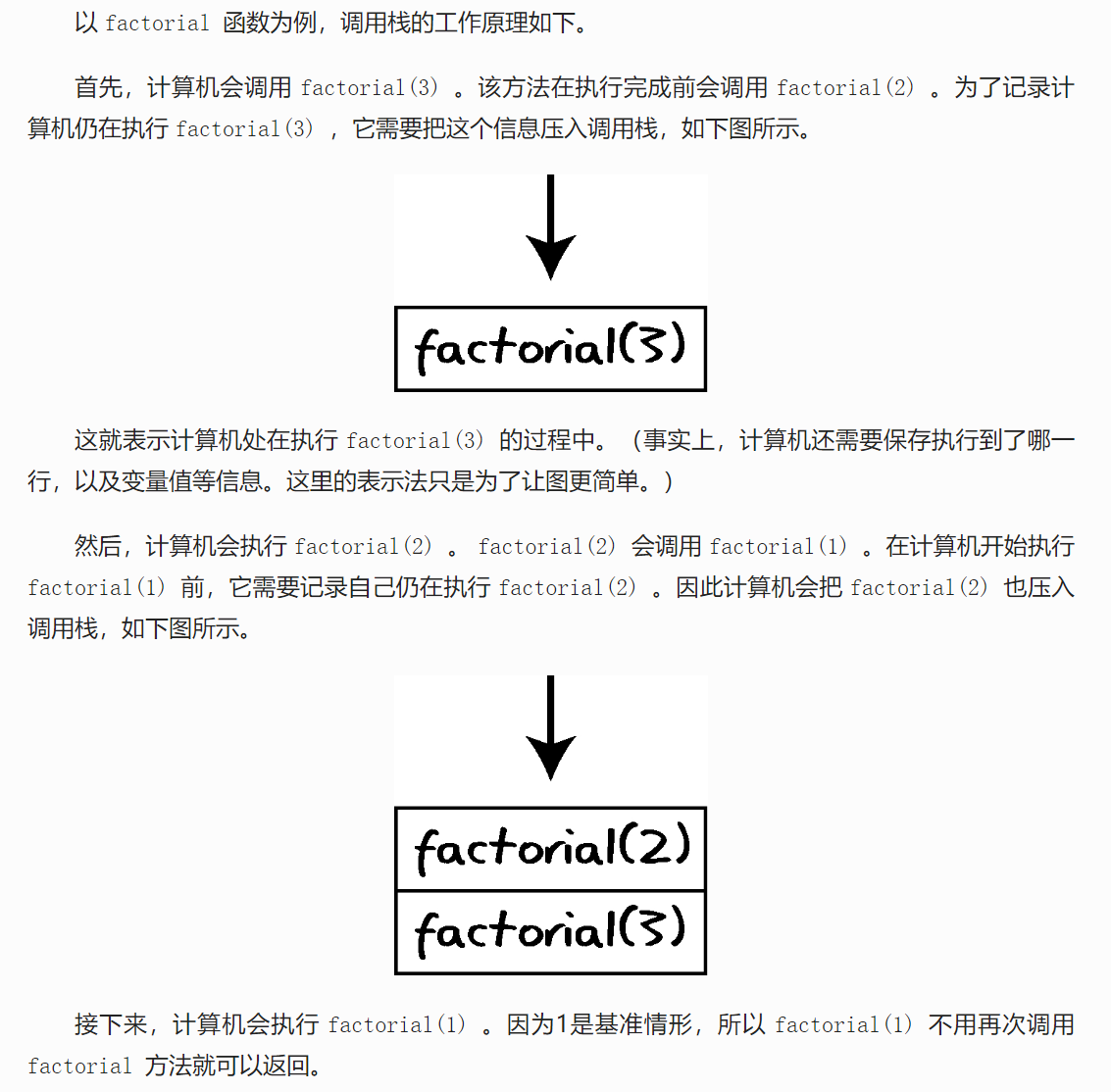
有个局部变量 number 记录当前值。

递归的应用场景

• 处理任意多层事情的场景，都可以考虑用递归。

• 当问题和子问题具有递推关系，比如杨辉三角、计算阶乘。

• 具有递归性质的数据结构，比如链表、树、图。

• 反向性问题，比如取反操作。

编程中 两种解决问题的思维

这个才是本文重点要学习的。

当面对未来未知的情况时，考虑使用使用自上而下解决问题的思维。

两种编写计算函数的方法:

• 自下而上(Bottom - Up)
  
  类似循环
• 自上而下 (Top - Down)
  
  递归思想

两者区别？

在计算函数时，自下而上和自上而下是两种不同的思维方式和实现策略：

在计算函数时，特别是像阶乘这样的递归函数，可以使用两种主要的实现方式来实现递归计算：自下而上（bottom-up）和自上而下（top-down）。这些方法各有优缺点，理解它们有助于选择适合的实现方式来解决特定的问题。以下是对这两种实现方式的解释：

自下而上（Bottom-Up）

自下而上方法，也称为 迭代方法 或 动态规划方法，是指从最小的子问题开始逐步构建解决方案，直到解决原始问题。这种方法通常用于动态规划算法中，但也可以用于一些简单的递归问题。

实现思路：

1. 定义最小问题: 从问题的最小子问题开始解决。例如，在计算阶乘时，可以从 0! 或 1! 开始。
2. 逐步构建: 使用迭代或循环逐步计算更大的问题的解。
3. 更新和存储: 将每个子问题的解存储起来，以便后续使用。

还是以计算阶乘的案例去介绍，自下而上实现方式：

def factorial_bottom_up(n):
    if n < 0:
        raise ValueError("Factorial is not defined for negative numbers")
    result = 1
    for i in range(2, n + 1):
        result *= i
    return result

# 示例用法
print(factorial_bottom_up(5))  # 输出 120

解释：

• 从 1 开始迭代计算 2 到 n 的阶乘。
• 通过逐步乘以每个数字来更新结果，最终得到 n!。

自上而下（Top-Down）

自上而下方法也称为 递归方法，是指从解决问题的最上层开始，递归地解决较小的子问题。这种方法在处理递归问题时非常自然（但可能存在重复计算的子问题，有些可以优化）。

实现思路：

1. 定义主问题: 从问题的最上层开始解决。
2. 递归分解: 将主问题递归地分解为较小的子问题。
3. 基本情况: 定义递归的基本情况，以停止递归。

还是以计算阶乘的案例，展示自上而下实现：

def factorial_top_down(n):
    if n < 0:
        raise ValueError("Factorial is not defined for negative numbers")
    if n == 0 or n == 1:
        return 1
    return n * factorial_top_down(n - 1)

# 示例用法
print(factorial_top_down(5))  # 输出 120

解释：

• 从 n 开始，递归调用 factorial_top_down(n - 1)，直到达到基本情况。
• 在基本情况时返回 1，逐层返回乘积结果。

总结

• 自下而上：通常是迭代的方法，逐步构建解决方案，适用于动态规划和需要避免重复计算的情况。它通常较为高效，尤其是在解决子问题重复计算时。

• 自上而下：通常是递归的方法，直观地解决问题，但可能会有较高的时间复杂度和空间复杂度，尤其在处理大规模问题时。(可以通过记忆化（Memoization）来优化性能)

自上而下的思考过程——求和案例

一般来说，自下而上的实现过程比较好理解，所以这里多列举一些自上而下的案例帮助思考，

自上而下的编程思考过程：

1. 把你正在写的函数想象成是别人实现过的函数。
2. 辨别子问题。
3. 看看你在子问题上调用函数时会发生什么，然后以此为基础继续。

求和案例

假设我们要写一个 sum 函数，计算数组中所有数的和。如果给函数传入数组[1，2，3，4，5]，那么它会返回这些数的和15。

我们需要做的第一件事就是想象已经有人实现了 sum 函数。（当然，你可能会有点难以接受，毕竟写函数是我们自己，怎么能假设别人写好了呢！ 但可以试着忘掉这一点，先假装 sum 函数已经实现好了。）

接下来，来辨别子问题。比起科学，这个过程更像是艺术，只要你多练习就能进步。 在这个例子中，可以认为子问题是数组[2，3，4，5]，即原数组中除第一个数以外的元素。

最后，来看看在子问题上调用 sum 函数会发生什么 ？

如果 sum 函数“已被正确实现”并且子问题是 [2，3，4，5]，那么调用 sum([2，3，4，5])时会发生什么呢?会得到2+3+4+5的和，也就是14。

而要求[1，2，3，4，5]的和，只需向 sum([2，3，4，5])的结果再加上1即可。

请使用编程语言实现一下：

mylist = [1, 2, 3, 4, 5]
def mysum(alist):

    if len(alist) == 1:
        return alist[0]
    else:
		# alist[-1] = alist[len(alist)-1]
        alist[0] += alist[-1]

    return mysum(alist[0:len(alist) - 1])

print(mysum(mylist))
# 15

台阶问题 案例

为什么需要用递归？

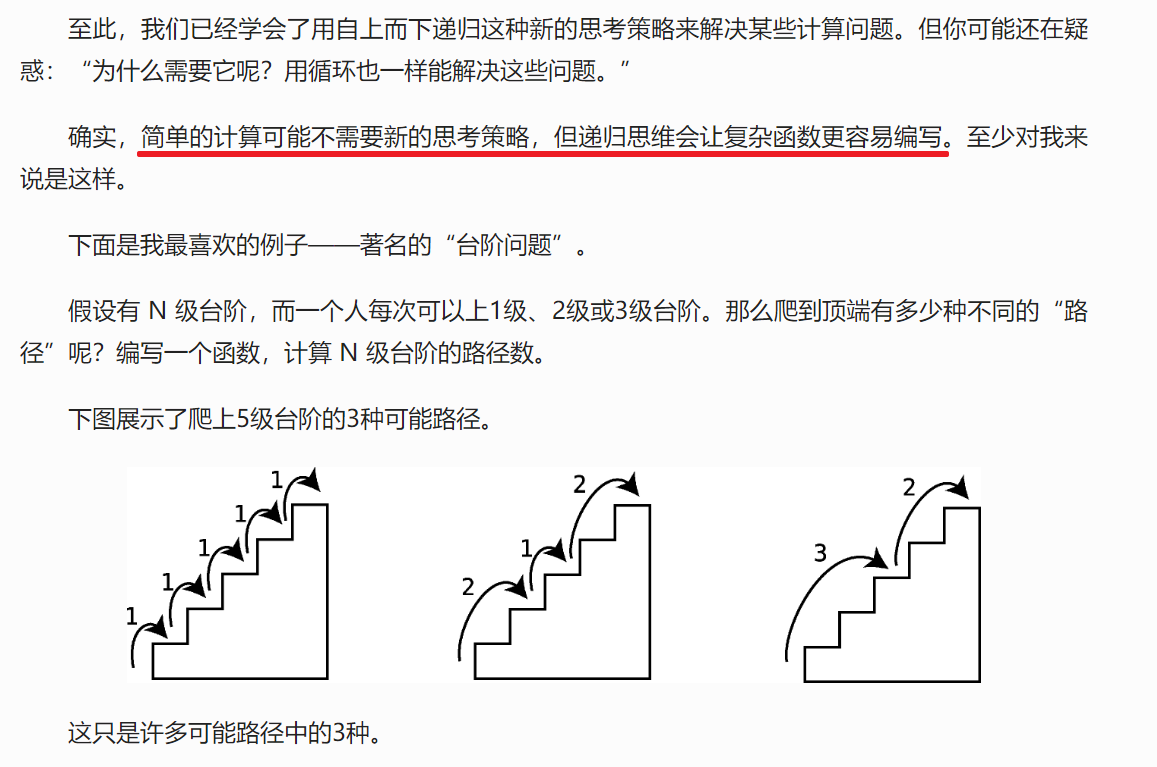
请写出代码：

todo

易位构词生成 案例

这个是一个很实用的案例，之前想将多个pyload 以不同位置组合成一个整体，就遇到这个难题。

请写出代码：

todo