P4221 [WC2018]州区划分 题解

题目链接

题目描述

给出 \(n\) 个城市，\(m\) 条边，一个划分合法当且仅当所有划分中的点集和集合中点之间存在的边集所构成的图不构成欧拉回路且联通。

定义一个点集的值为

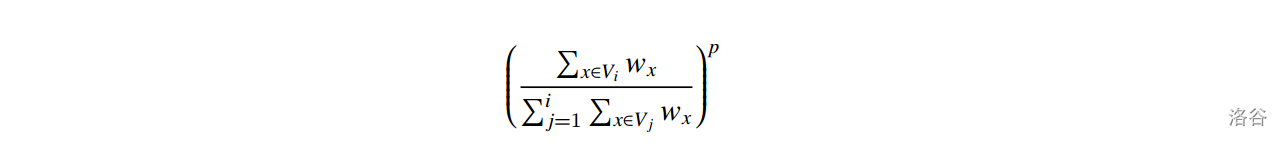
划分的总值为其中所有点集的值之积，求所有合法划分的值之和。

题目分析

看到数据范围以及题目描述，不难想到使用状压 dp 解决此问题，首先对于每种状态判断是否合法，再枚举当前总状态和最后一个加进来的状态。

设当前状态为 \(i\)，枚举出的子集状态为 \(j\)，保证其合法，状态集合大小记为 \(siz_i\)，可以得到以下状态转移方程：

\(f_i=\sum_{i\bigcap j=j}f_j(\frac{siz_j}{siz_i})^p\)

时间复杂度为 \(O(3^n)\)，还无法通过本题。

继续观察柿子，如果把后面的乘数拆开分别处理，一个放到等式左边，一个另起一个函数，就会发现这其实就是一个子集卷积，卷完左边后对于右边部分乘上逆元恢复就行。

还有一个问题，这个柿子中 \(f\) 会自己卷自己，不过发现卷积中只会用到比自己 1 的个数少的状态，只需要一边卷一边处理即可。

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#define N 35
#define ll long long
using namespace std;
ll e,head[50000],nex[50000],to[50000];
ll val[N],g[22][(1<<22)];
ll vis[N],f[22][(1<<22)];
ll inv[(1<<22)];
ll n;
const ll mod=998244353;
queue<ll> q;
ll qp(ll x,ll y){
	ll ans=1;
	while(y){
		if(y&1) ans=(ans*x)%mod;
		x=(x*x)%mod;
		y>>=1;
	}
	return ans;
}
void add(ll u,ll v){
	to[++e]=v;nex[e]=head[u];head[u]=e;
	to[++e]=u;nex[e]=head[v];head[v]=e;
}
bool jud(ll x){
	if(x==0) return false;
	while(q.size()) q.pop();
	for(ll i=1;i<=n;i++) vis[i]=0;
	for(ll i=1;i<=n;i++)if((1<<(i-1))&x){q.push(i);break;}
	while(q.size()){
		ll u=q.front();q.pop();if(vis[u])continue;vis[u]++;
		for(int i=head[u];i;i=nex[i]){
			int v=to[i];
			if((1<<(v-1))&x && !vis[v]) q.push(v);
		}
	}
	for(ll i=0;i<n;i++) if((1<<i)&x && !vis[i+1]) return true;
	for(ll i=0;i<=n;i++){
		if(x&(1<<i)){
			int cnt=0;
			for(ll j=head[i+1];j;j=nex[j]){
				ll v=to[j];
				if((1<<(v-1))&x) cnt++;
			}
			if(cnt%2) return true;
		}
	}
	return false;
}
ll sum(ll x){
	ll ans=0;
	for(ll i=0;i<n;i++) if(x&(1<<i)) ans+=val[i+1];
	return ans;
}
void fwt(ll *f,ll opt){
	for(ll mid=1,R=2;R<=(1<<n);R<<=1,mid<<=1){
		for(ll j=0;j<(1<<n);j+=R){
			for(ll k=0;k<mid;k++){
				if(opt==1) f[j+k+mid]=(f[j+k+mid]+f[j+k])%mod;
				else f[j+k+mid]=(f[j+k+mid]-f[j+k]+mod)%mod;
			}
		}
	}
}
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return x*f;
}
int main(){
	ll m,p,u,v;
	n=read();m=read();p=read();
	for(ll i=1;i<=m;i++){
		u=read();v=read();
		add(u,v);
	}
	for(ll i=0;i<n;i++) val[i+1]=read();
	for(ll i=0;i<(1<<n);i++){
		if(jud(i)) g[__builtin_popcount(i)][i]=qp(sum(i),p);
		inv[i]=qp(qp(sum(i),mod-2),p);
	}
	f[0][0]=1;fwt(f[0],1);
	for(ll i=0;i<=n;i++) fwt(g[i],1);
	for(ll i=1;i<=n;i++){
		for(ll j=0;j<i;j++){
			for(ll k=0;k<(1<<n);k++){
				f[i][k]+=(f[j][k]*g[i-j][k])%mod;
				f[i][k]%=mod;
			}
		}
		fwt(f[i],-1);
		for(ll j=0;j<(1<<n);j++){
			if(__builtin_popcount(j)==i)f[i][j]=(f[i][j]*inv[j])%mod;
			else f[i][j]=0;
		}
		if(i!=n)fwt(f[i],1);
	}
	cout<<f[n][(1<<n)-1];
}