tensorflow解决回归问题简单案列

1 待拟合函数

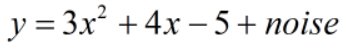
noise服从均值为0，方差为15的正太分布，即noise ~ N(0,15)。

2 基于模型的训练

根据散点图分布特点，猜测原始数据是一个二次函数模型，如下：

其中，a,b,c为待训练参数

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

x=np.linspace(-10,10,200) #生成200个随机点
noise=np.random.normal(0,15,x.shape) #生成噪声
y=3*np.square(x)+4*x-5+noise

a=tf.Variable(.0)
b=tf.Variable(.0)
c=tf.Variable(.0)
y_=a*np.square(x)+b*x+c #构造一个非线性模型

loss=tf.reduce_mean(tf.square(y-y_))#二次代价函数

optimizer=tf.train.AdamOptimizer(0.2) #Adam自适应学习率优化器

train=optimizer.minimize(loss) #最小化代价函数
init=tf.global_variables_initializer() #变量初始化
with tf.Session() as sess:
    sess.run(init)
    for epoch in range(601):
        sess.run(train)
        if epoch>0 and epoch%100==0:
            print(epoch,sess.run([a,b,c]),"mse:",sess.run(loss))
    pre=sess.run(y_)
    plt.figure()
    plt.scatter(x,y)
    plt.plot(x,pre,'-r',lw=4)
    plt.show()

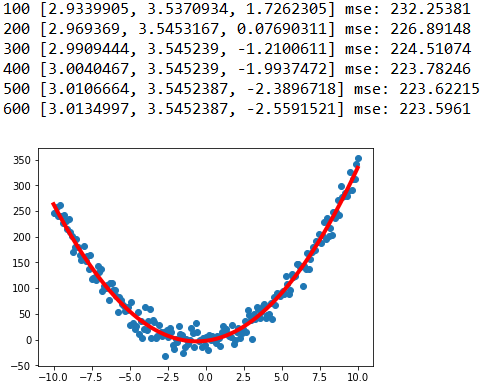
经过600次训练后得到二次函数模型如下：

3 基于网络的训练

网络结构如下：

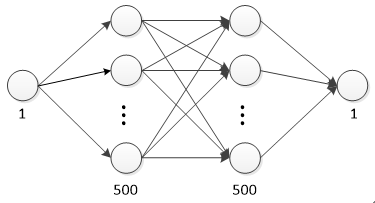
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

x=np.linspace(-10,10,200)[:,np.newaxis] #生成200个随机点
noise=np.random.normal(0,15,x.shape) #生成噪声
y=3*np.square(x)+4*x-5+noise

x_=tf.placeholder(tf.float32,[None,1]) #定义placeholder
y_=tf.placeholder(tf.float32,[None,1]) #定义placeholder

#定义神经网络中间层(layer_1)
w1=tf.Variable(tf.random_normal([1,500]))
b1=tf.Variable(tf.zeros([500]))
z1=tf.matmul(x_,w1)+b1
a1=tf.nn.relu(z1)

#定义神经网络中间层(layer_2)
w2=tf.Variable(tf.random_normal([500,500]))
b2=tf.Variable(tf.zeros([500]))
z2=tf.matmul(a1,w2)+b2
a2=tf.nn.relu(z2)

#定义神经网络输出层
w3=tf.Variable(tf.random_normal([500,1]))
b3=tf.Variable(tf.zeros([1]))
z3=tf.matmul(a2,w3)+b3

loss=tf.reduce_mean(tf.square(y_-z3))#二次代价函数

optimizer=tf.train.FtrlOptimizer(0.2) #Ftrl优化器

train=optimizer.minimize(loss) #最小化代价函数
init=tf.global_variables_initializer() #变量初始化
with tf.Session() as sess:
    sess.run(init)
    for epoch in range(6001):
        sess.run(train,feed_dict={x_:x,y_:y})
        if epoch>0 and epoch%1000==0:
            mse=sess.run(loss,feed_dict={x_:x,y_:y})
            print(epoch,mse)
    pre=sess.run(z3,feed_dict={x_:x,y_:y})
    plt.figure()
    plt.scatter(x,y)
    plt.plot(x,pre,'-r',lw=4)
    plt.show()

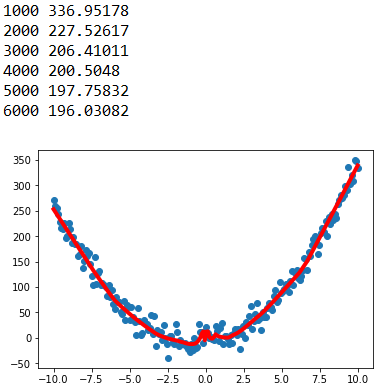
注意：在网络出口处不要加上sigmoid、tanh、relu激活函数进行非线性变换，因为sigmoid函数会将回归值压缩到(0,1)，tanh函数会将回归值压缩到(-1,1)，relu函数会将回归值映射到(0,+oo)，而真实值没有这些限制，导致损失函数的计算不合理，误差反馈较慢，模型不收敛。

另外，可以先将真实值y归一化，记为y1，再将回归值z3与z1比较，计算误差并调节网络权值和偏值，将z3逆归一化的值作为网络预测值。

5 常用优化器

#1.梯度下降优化器
optimizer=tf.train.GradientDescentOptimizer(0.2)
#2.自适应学习率优化器
optimizer=tf.train.AdagradOptimizer(0.2)
#3.自适应学习率优化器
optimizer=tf.train.RMSPropOptimizer(0.2)
#4.Adam自适应学习率优化器
optimizer=tf.train.AdamOptimizer(0.2)
#5.Adadelta优化器
optimizer=tf.train.AdadeltaOptimizer(0.2)
#6.Proximal梯度下降优化器
optimizer=tf.train.ProximalGradientDescentOptimizer(0.2)
#7.Proximal自适应学习率优化器
optimizer=tf.train.ProximalAdagradOptimizer(0.2)
#8.Ftrl优化器
optimizer=tf.train.FtrlOptimizer(0.2)

​ 声明：本文转自tensorflow解决回归问题简单案列