BZOJ4016：[FJOI2014]最短路径树问题
浅谈树分治：https://www.cnblogs.com/AKMer/p/10014803.html
题目传送门：https://www.lydsy.com/JudgeOnline/problem.php?id=4016
很讨厌这种把两个模板强行合在一起的出题人。。。
求出最短路之后按字典序去递归建树就是字典序最小的最短路径树。
然后\(f[i][0]\)表示扫过的子树里，经过\(i\)个点可以得到的最长长度，\(f[i][1]\)表示方案数。\(g\)数组同理，不过存的是当前子树的，然后维护一下随便搞搞就\(A\)了。
点分治写起来很顺手，边分治就贼有趣了哟。。。如果你继续用上面那个表示意义，就会被下面这张图卡掉（除非你冒着\(TLE\)的风险不重新建树）：
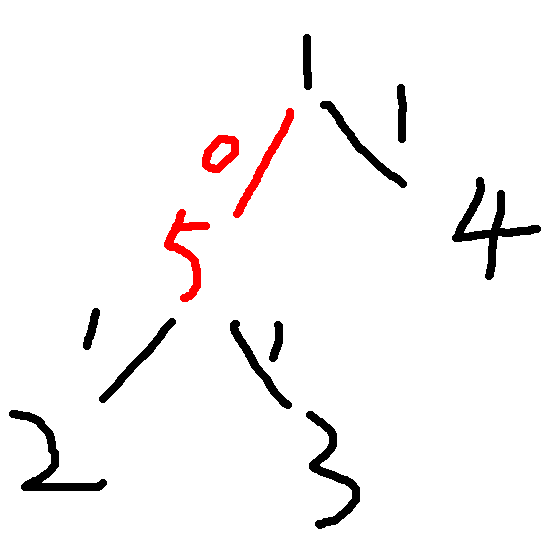
\(2-1-3\)这条路径会在点分做法下被忽视，所以\(f\)数组和\(g\)数组的第一个下标应该由表示点变成表示边，这样才不会被卡。可以保证，如果两条原树边之间全是新加边，那么这两条原树边在原树上肯定是靠在一起的。
时间复杂度：\(O(nlogn)\)
空间复杂度：\(O(n)\)
点分治版代码：
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int,int> pii;
#define fr first
#define sc second
const int maxn=3e4+5,maxm=6e4+5;
int n,m,limit;
int dis[maxn];
vector<pii>to[maxn];
int read() {
int x=0,f=1;char ch=getchar();
for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
for(;ch>='0'&&ch<='9';ch=getchar())x=x*10+ch-'0';
return x*f;
}
namespace Pre {
int tot;
int now[maxn],son[maxm*2],pre[maxm*2],val[maxm*2];
void add(int a,int b,int c) {
pre[++tot]=now[a];
now[a]=tot,son[tot]=b,val[tot]=c;
}
struct node {
int u,dis;
node() {}
node(int _u,int _dis) {
u=_u,dis=_dis;
}
bool operator<(const node &a)const {
return dis<a.dis;
}
};
struct Heap {
int tot;
node tree[maxm];
void ins(node u) {
tree[++tot]=u;
int pos=tot;
while(pos>1) {
if(tree[pos]<tree[pos>>1])
swap(tree[pos],tree[pos>>1]),pos>>=1;
else break;
}
}
node pop() {
node res=tree[1];
tree[1]=tree[tot--];
int pos=1,son=2;
while(son<=tot) {
if(son<tot&&tree[son|1]<tree[son])son|=1;
if(tree[son]<tree[pos])
swap(tree[son],tree[pos]),pos=son,son=pos<<1;
else break;
}
return res;
}
}T;
void dijstra() {
memset(dis,0x3f,sizeof(dis));
dis[1]=0,T.ins(node(1,0));
while(T.tot) {
node tmp=T.pop();int u=tmp.u;
if(dis[u]<tmp.dis)continue;
for(int p=now[u],v=son[p];p;p=pre[p],v=son[p])
if(dis[v]>dis[u]+val[p]) {
dis[v]=dis[u]+val[p];
T.ins(node(v,dis[v]));
}
}
}
void init() {
n=read(),m=read(),limit=read();
for(int i=1;i<=m;i++) {
int a=read(),b=read(),c=read();
add(a,b,c),add(b,a,c);
}dijstra();
for(int i=1;i<=n;i++) {
for(int p=now[i],v=son[p];p;p=pre[p],v=son[p])
if(dis[v]==dis[i]+val[p])to[i].push_back(make_pair(v,val[p]));
}
}
}
namespace point_divide {
int siz[maxn];
bool vis[maxn];
int f[maxn][2],g[maxn][2];
int tot,N,mx,rt,ans1,ans2;
int now[maxn],pre[maxn*2],son[maxn*2],val[maxn*2];
void add(int a,int b,int c) {
pre[++tot]=now[a];
now[a]=tot,son[tot]=b,val[tot]=c;
}
void build(int u) {
vis[u]=1;if(to[u].empty())return;
vector<pii>::iterator it;
sort(to[u].begin(),to[u].end());
for(it=to[u].begin();it!=to[u].end();it++) {
pii tmp=*it;
if(vis[tmp.fr])continue;
add(u,tmp.fr,tmp.sc);
add(tmp.fr,u,tmp.sc);
build(tmp.fr);
}
}
void find_rt(int fa,int u) {
int res=0;siz[u]=1;
for(int p=now[u],v=son[p];p;p=pre[p],v=son[p])
if(!vis[v]&&v!=fa)find_rt(u,v),siz[u]+=siz[v],res=max(res,siz[v]);
res=max(res,N-siz[u]);
if(res<mx)mx=res,rt=u;
}
void make_g(int fa,int u,int dep,int len) {
if(dep<limit) {
if(len>g[dep][0])g[dep][0]=len,g[dep][1]=0;
if(len==g[dep][0])g[dep][1]++;
}siz[u]=1;
for(int p=now[u],v=son[p];p;p=pre[p],v=son[p])
if(!vis[v]&&v!=fa)make_g(u,v,dep+1,len+val[p]),siz[u]+=siz[v];
}
void work(int u,int size) {
N=size,mx=rt=n+1,find_rt(0,u);
u=rt,vis[u]=1;
for(int p=now[u],v=son[p];p;p=pre[p],v=son[p])
if(!vis[v]){
make_g(u,v,1,val[p]);
for(int i=1;i<limit;i++) {
if(g[i][0]+f[limit-i-1][0]>ans1)ans1=g[i][0]+f[limit-i-1][0],ans2=0;
if(g[i][0]+f[limit-i-1][0]==ans1)ans2+=g[i][1]*f[limit-i-1][1];
}
for(int i=1;i<limit;i++) {
if(g[i][0]>f[i][0])f[i][0]=g[i][0],f[i][1]=0;
if(g[i][0]==f[i][0])f[i][1]+=g[i][1];
g[i][0]=g[i][1]=0;
}
}
for(int i=1;i<=limit;i++)
f[i][0]=f[i][1]=0;
for(int p=now[u],v=son[p];p;p=pre[p],v=son[p])
if(!vis[v])work(v,siz[v]);
}
void fake() {
build(1);memset(vis,0,sizeof(vis));f[0][1]=1;
work(1,n);printf("%d %d\n",ans1,ans2);
}
}
int main() {
Pre::init();
point_divide::fake();
return 0;
}
边分治版代码如下：
#include <cmath>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int,int> pii;
#define fr first
#define sc second
const int maxn=6e4+5,maxm=6e4+5;
int dis[maxn];
int cnt,n,m,limit;
vector<pii>to[maxn];
int read() {
int x=0,f=1;char ch=getchar();
for(;ch<'0'||ch>'9';ch=getchar())if(ch=='-')f=-1;
for(;ch>='0'&&ch<='9';ch=getchar())x=x*10+ch-'0';
return x*f;
}
namespace Pre {
int tot;
int now[maxn],son[maxm*2],pre[maxm*2],val[maxm*2];
void add(int a,int b,int c) {
pre[++tot]=now[a];
now[a]=tot,son[tot]=b,val[tot]=c;
}
struct node {
int u,dis;
node() {}
node(int _u,int _dis) {
u=_u,dis=_dis;
}
bool operator<(const node &a)const {
return dis<a.dis;
}
};
struct Heap {
int tot;
node tree[maxm];
void ins(node u) {
tree[++tot]=u;
int pos=tot;
while(pos>1) {
if(tree[pos]<tree[pos>>1])
swap(tree[pos],tree[pos>>1]),pos>>=1;
else break;
}
}
node pop() {
node res=tree[1];
tree[1]=tree[tot--];
int pos=1,son=2;
while(son<=tot) {
if(son<tot&&tree[son|1]<tree[son])son|=1;
if(tree[son]<tree[pos])
swap(tree[son],tree[pos]),pos=son,son=pos<<1;
else break;
}
return res;
}
}T;
void dijstra() {
memset(dis,0x3f,sizeof(dis));
dis[1]=0,T.ins(node(1,0));
while(T.tot) {
node tmp=T.pop();int u=tmp.u;
if(dis[u]<tmp.dis)continue;
for(int p=now[u],v=son[p];p;p=pre[p],v=son[p])
if(dis[v]>dis[u]+val[p]) {
dis[v]=dis[u]+val[p];
T.ins(node(v,dis[v]));
}
}
}
void init() {
cnt=n=read(),m=read(),limit=read()-1;
for(int i=1;i<=m;i++) {
int a=read(),b=read(),c=read();
add(a,b,c),add(b,a,c);
}dijstra();
for(int i=1;i<=n;i++) {
for(int p=now[i],v=son[p];p;p=pre[p],v=son[p])
if(dis[v]==dis[i]+val[p])to[i].push_back(make_pair(v,val[p]));
}
}
}
namespace edge_divide {
int siz[maxn];
bool vis[maxn];
int f[maxn][2],g[maxn][2];
int tot,N,mx,id,ans1,ans2;
int now[maxn],pre[maxn*2],son[maxn*2],val[maxn*2];
void add(int a,int b,int c) {
pre[++tot]=now[a];
now[a]=tot,son[tot]=b,val[tot]=c;
}
void build(int u) {
vis[u]=1;if(to[u].empty())return;
vector<pii>::iterator it;
sort(to[u].begin(),to[u].end());
for(it=to[u].begin();it!=to[u].end();it++) {
pii tmp=*it;
if(vis[tmp.fr])continue;
add(u,tmp.fr,tmp.sc);
add(tmp.fr,u,tmp.sc);
build(tmp.fr);
}
to[u].clear();
}
void find_son(int fa,int u) {
for(int p=now[u],v=son[p];p;p=pre[p],v=son[p])
if(v!=fa)to[u].push_back(make_pair(v,val[p])),find_son(u,v);
}
void rebuild() {
vector<pii>::iterator it;
tot=1;memset(now,0,sizeof(now));
for(int i=1;i<=cnt;i++) {
int size=to[i].size();
if(size<=2) {
for(it=to[i].begin();it!=to[i].end();it++) {
pii tmp=*it;
add(i,tmp.fr,tmp.sc),add(tmp.fr,i,tmp.sc);
}
}
else {
pii u1=make_pair(++cnt,0),u2;
if(size==3)u2=to[i].front();
else u2=make_pair(++cnt,0);
add(i,u1.fr,u1.sc),add(u1.fr,i,u1.sc);
add(i,u2.fr,u2.sc),add(u2.fr,i,u2.sc);
if(size==3) {
for(int j=1;j<=2;j++)
to[cnt].push_back(to[i].back()),to[i].pop_back();
}
else {
int p=0;
for(it=to[i].begin();it!=to[i].end();it++) {
if(!p)to[cnt-1].push_back(*it);
else to[cnt].push_back(*it);p^=1;
}
}
}
}
}
void find_edge(int fa,int u) {
siz[u]=1;
for(int p=now[u],v=son[p];p;p=pre[p],v=son[p])
if(!vis[p>>1]&&v!=fa) {
find_edge(u,v),siz[u]+=siz[v];
if(abs(N-2*siz[v])<mx)
mx=abs(N-2*siz[v]),id=p>>1;
}
}
void solve1(int fa,int u,int dep,int len,bool bo) {
if(dep<limit&&bo) {
if(len>f[dep][0])f[dep][0]=len,f[dep][1]=0;
if(len==f[dep][0])f[dep][1]++;
}siz[u]=1;
for(int p=now[u],v=son[p];p;p=pre[p],v=son[p])
if(!vis[p>>1]&&v!=fa)
solve1(u,v,dep+(val[p]>0),len+val[p],val[p]),siz[u]+=siz[v];
}
void solve2(int fa,int u,int dep,int len,bool bo) {
if(dep<limit&&bo) {
if(len>g[dep][0])g[dep][0]=len,g[dep][1]=0;
if(len==g[dep][0])g[dep][1]++;
}siz[u]=1;
for(int p=now[u],v=son[p];p;p=pre[p],v=son[p])
if(!vis[p>>1]&&v!=fa)
solve2(u,v,dep+(val[p]>0),len+val[p],val[p]),siz[u]+=siz[v];
}
void work(int u,int size) {
if(size<2)return;
N=size,mx=id=cnt+1,find_edge(0,u);
vis[id]=1;int u1=son[id<<1],u2=son[id<<1|1];
solve1(0,u1,0,0,0),solve2(0,u2,0,0,0);
for(int i=0;i<=limit-(val[id<<1]>0);i++) {
if(g[i][0]+f[limit-i-(val[id<<1]>0)][0]+val[id<<1]>ans1)
ans1=g[i][0]+f[limit-i-(val[id<<1]>0)][0]+val[id<<1],ans2=0;
if(g[i][0]+f[limit-i-(val[id<<1]>0)][0]+val[id<<1]==ans1)
ans2+=g[i][1]*f[limit-i-(val[id<<1]>0)][1];
}
for(int i=0;i<limit;i++)
g[i][0]=f[i][0]=g[i][1]=f[i][1]=0;
g[0][1]=f[0][1]=1;
work(u1,siz[u1]),work(u2,siz[u2]);
}
void fake() {
build(1);memset(vis,0,sizeof(vis));
find_son(0,1),rebuild();f[0][1]=g[0][1]=1;
work(1,cnt);printf("%d %d\n",ans1,ans2);
}
}
int main() {
Pre::init();
edge_divide::fake();
return 0;
}
BZOJ4016：[FJOI2014]最短路径树问题的更多相关文章
- [BZOJ4016][FJOI2014]最短路径树问题
[BZOJ4016][FJOI2014]最短路径树问题 试题描述 给一个包含n个点,m条边的无向连通图.从顶点1出发,往其余所有点分别走一次并返回. 往某一个点走时,选择总长度最短的路径走.若有多条长 ...
- [BZOJ4016][FJOI2014]最短路径树问题(dijkstra+点分治)
4016: [FJOI2014]最短路径树问题 Time Limit: 5 Sec Memory Limit: 512 MBSubmit: 1796 Solved: 625[Submit][Sta ...
- 【BZOJ4016】[FJOI2014]最短路径树问题
[BZOJ4016][FJOI2014]最短路径树问题 题面 bzoj 洛谷 题解 虽然调了蛮久,但是思路还是蛮简单的2333 把最短路径树构出来,然后点分治就好啦 ps:如果树构萎了,这组数据可以卡 ...
- 【BZOJ4016】[FJOI2014]最短路径树问题 最短路径树+点分治
[BZOJ4016][FJOI2014]最短路径树问题 Description 给一个包含n个点,m条边的无向连通图.从顶点1出发,往其余所有点分别走一次并返回. 往某一个点走时,选择总长度最短的路径 ...
- 【BZOJ4016】[FJOI2014]最短路径树问题（点分治，最短路）
[BZOJ4016][FJOI2014]最短路径树问题(点分治,最短路) 题面 BZOJ 洛谷 题解 首先把最短路径树给构建出来,然后直接点分治就行了. 这个东西似乎也可以长链剖分,然而没有必要. # ...
- bzoj 4016 [FJOI2014]最短路径树问题（最短路径树+树分治）
4016: [FJOI2014]最短路径树问题 Time Limit: 5 Sec Memory Limit: 512 MBSubmit: 426 Solved: 147[Submit][Stat ...
- BZOJ_4016_[FJOI2014]最短路径树问题_最短路+点分治
BZOJ_4016_[FJOI2014]最短路径树问题_最短路+点分治 Description 给一个包含n个点,m条边的无向连通图.从顶点1出发,往其余所有点分别走一次并返回. 往某一个点走时,选择 ...
- 【BZOJ-4016】最短路径树问题 Dijkstra + 点分治
4016: [FJOI2014]最短路径树问题 Time Limit: 5 Sec Memory Limit: 512 MBSubmit: 1092 Solved: 383[Submit][Sta ...
- [FJOI2014]最短路径树问题 长链剖分
[FJOI2014]最短路径树问题 LG传送门 B站传送门 长链剖分练手好题. 如果你还不会长链剖分的基本操作,可以看看我的总结. 这题本来出的很没水平,就是dijkstra(反正我是不用SPFA)的 ...
- 洛谷 [FJOI2014]最短路径树问题 解题报告
[FJOI2014]最短路径树问题 题目描述 给一个包含\(n\)个点,\(m\)条边的无向连通图.从顶点\(1\)出发,往其余所有点分别走一次并返回. 往某一个点走时,选择总长度最短的路径走.若有多 ...
随机推荐
- windows下如何快速优雅的使用python的科学计算库？
Python是一种强大的编程语言,其提供了很多用于科学计算的模块,常见的包括numpy.scipy.pandas和matplotlib.要利用Python进行科学计算,就需要一一安装所需的模块,而这些 ...
- 现在有一张半径为r的圆桌，其中心位于(x,y)，现在他想把圆桌的中心移到(x1,y1)。每次移动一步，都必须在圆桌边缘固定一个点然后将圆桌绕这个点旋转。问最少需要移动几步。
// ConsoleApplication5.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h" #include<vector> ...
- pooler [转]
pooler和poolboy都是用erlang写的管理进程池的库. pooler/poolboygithub : seth/pooler · GitHubgithub : devinus/poolbo ...
- OpenCV 中的三大数据类型( 概述 )
前言 OpenCV 提供了许多封装好了的类型,而其中,以三大类型最为核心.本文将大致介绍这三大类型. CvArr:不确定数组 它可以被视为一个抽象基类,后面的两大类型都继承此类型并扩展.只要某个函数的 ...
- JavaScript学习3：原型和继承
原型 我们创建的每个函数都有一个prototype(原型)属性,这个属性是一个对象,它的用途是包括能够由特定类型的全部实例共享的属性和方法.逻辑上能够这么理解:prototype是通过调用构造函数而创 ...
- 【转】android 签名验证防止重打包
网上资料很多,这里只做一个笔记反编译 dex 修改重新打包签名后 apk 的签名信息肯定会改变,所以可以在代码中判断签名信息是否被改变过,如果签名不一致就退出程序,以防止 apk 被重新打包. 1 j ...
- Android—— 4.2 Vold挂载管理_NetlinkManager (四)
在前文Android-- 4.2 Vold挂载管理_主体构建main (一)中有结构图表示,Vold是kernel与用户层的一个交互管理模块. Android-- 4.2 Vold挂载管理_Volum ...
- ajax学习笔记(3)--$.get()方法
<head runat="server"> <title>jQuery中的$.get()方法</title> <script src=&q ...
- jvm堆查看
jps查看jvm的进程号 jmap -histo:live [进程号] >log.txt dump jvm堆.
- 性能测试--yslow
YSlow YSlow可以对网站的页面进行分析,并告诉你为了提高网站性能,如何基于某些规则而进行优化. YSlow可以分析任何网站,并为每一个规则产生一个整体报告,如果页面可以进行优化,则YSlow会 ...