【bzoj3601】一个人的数论 莫比乌斯反演+高斯消元

题目描述

---

题解

莫比乌斯反演+高斯消元

（前方高能：所有题目中给出的幂次d，公式里为了防止混淆，均使用了k代替）

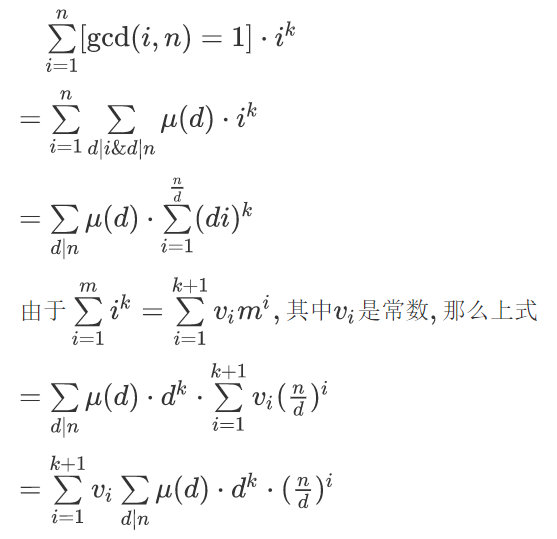
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const ll mod = 1000000007;
ll a[110][110] , p[1010] , v[1010];
ll pow(ll x , ll y)
{
	ll ans = 1;
	while(y)
	{
		if(y & 1) ans = ans * x % mod;
		x = x * x % mod , y >>= 1;
	}
	return ans;
}
int main()
{
	int d , w , i , j , k;
	ll t , ans = 0;
	scanf("%d%d" , &d , &w);
	for(i = 1 ; i <= w ; i ++ ) scanf("%lld%lld" , &p[i] , &v[i]);
	if(w == 1 && p[1] == 1)
	{
		puts("1");
		return 0;
	}
	for(i = 1 ; i <= d + 1 ; i ++ )
	{
		a[i][0] = 1;
		for(j = 1 ; j <= d + 1 ; j ++ ) a[i][j] = a[i][j - 1] * i % mod;
		a[i][d + 2] = (a[i - 1][d + 2] + a[i][d]) % mod;
	}
	for(i = 1 ; i <= d + 1 ; i ++ )
	{
		for(j = i ; j <= d + 1 ; j ++ ) if(a[i][j]) break;
		if(j > d + 1) continue;
		for(k = i ; k <= d + 2 ; k ++ ) swap(a[i][k] , a[j][k]);
		t = pow(a[i][i] , mod - 2);
		for(j = i ; j <= d + 2 ; j ++ ) a[i][j] = a[i][j] * t % mod;
		for(j = 1 ; j <= d + 1 ; j ++ )
			if(j != i)
				for(t = a[j][i] , k = i ; k <= d + 2 ; k ++ )
					a[j][k] = (a[j][k] - a[i][k] * t % mod + mod) % mod;
	}
	for(i = 1 ; i <= d + 1 ; i ++ )
	{
		t = 1;
		for(j = 1 ; j <= w ; j ++ )
			t = t * pow(pow(p[j] , v[j]) , i) % mod * (1 - pow(p[j] , (d - i + mod - 1) % (mod - 1)) + mod) % mod;
		ans = (ans + a[i][d + 2] * t) % mod;
	}
	printf("%lld\n" , ans);
	return 0;
}