BZOJ1415 [Noi2005]聪聪和可可【SPFA + 期望dp记忆化搜索】

题目

输入格式

数据的第1行为两个整数N和E，以空格分隔，分别表示森林中的景点数和连接相邻景点的路的条数。第2行包含两个整数C和M，以空格分隔，分别表示初始时聪聪和可可所在的景点的编号。接下来E行，每行两个整数，第i+2行的两个整数Ai和Bi表示景点Ai和景点Bi之间有一条路。所有的路都是无向的，即：如果能从A走到B，就可以从B走到A。输入保证任何两个景点之间不会有多于一条路直接相连，且聪聪和可可之间必有路直接或间接的相连。

输出格式

输出1个实数，四舍五入保留三位小数，表示平均多少个时间单位后聪聪会把可可吃掉。

输入样例

【输入样例1】

4 3

1 4

1 2

2 3

3 4

【输入样例2】

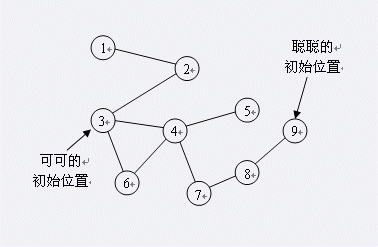
9 9

9 3

1 2

2 3

3 4

4 5

3 6

4 6

4 7

7 8

8 9

输出样例

【输出样例1】

1.500

【输出样例2】

2.167

提示

【样例说明1】

开始时，聪聪和可可分别在景点1和景点4。

第一个时刻，聪聪先走，她向更靠近可可(景点4)的景点走动，走到景点2，然后走到景点3；假定忽略走路所花时间。

可可后走，有两种可能：

第一种是走到景点3，这样聪聪和可可到达同一个景点，可可被吃掉，步数为1，概率为。

第二种是停在景点4，不被吃掉。概率为。

到第二个时刻，聪聪向更靠近可可(景点4)的景点走动，只需要走一步即和可可在同一景点。因此这种情况下聪聪会在两步吃掉可可。

所以平均的步数是1* +2* =1.5步。

对于所有的数据，1≤N,E≤1000。

对于50%的数据，1≤N≤50。

题解

讲实在的不难写，但是概率这种玩意写起来总是很蛋疼【蒟蒻跪倒】

由于聪聪的走法是唯一的、可求的，我们不妨令$p[i][j]$表示聪聪在i号点，可可在j号点时聪聪的下一步位置

由于$n<=1000$，我们可以用SPFA求出从每个点u出发所有点到达该点最短路的上一个节点，即为每个点出发到u点的下一个节点

现在我们有了p[][]，就很好求了

我们设$f[i][j]$表示聪聪在i号点，可可在j号点的期望步数

若$i == j$，聪聪可可在一起，$f[i][j] = 0$

若$p[i][j] == j$或$p[p[i][j]][j]==j$，可以一次性走到，$f[i][j] = 1$

否则令$t = p[p[i][j]][j]$，枚举j的邻点v，$f[i][j]=\frac{f[t][j] + \sum{f[t][v]}}{degree_j + 1} + 1$

记忆化搜索解决

#include<iostream>

#include<cmath>

#include<cstdio>

#include<cstring>

#include<queue>

#include<algorithm>

#define LL long long int

#define REP(i,n) for (int i = 1; i <= (n); i++)

#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)

using namespace std;

const int maxn = 1005,maxm = 2000005,INF = 1000000000;

inline int read(){

	int out = 0,flag = 1; char c = getchar();

	while (c < 48 || c > 57) {if (c == '-') flag = -1; c = getchar();}

	while (c >= 48 && c <= 57) {out = (out << 3) + (out << 1) + c - '0'; c = getchar();}

	return out * flag;

}

int p[maxn][maxn],isc[maxn][maxn],d[maxn],vis[maxn],pre[maxn],de[maxn];

double f[maxn][maxn];

int h[maxn],ne = 2,n,m,cc,kk;

struct EDGE{int to,nxt;}ed[maxm];

void build(int u,int v){

	de[u]++; de[v]++;

	ed[ne] = (EDGE){v,h[u]}; h[u] = ne++;

	ed[ne] = (EDGE){u,h[v]}; h[v] = ne++;

}

queue<int> q;

void spfa(int S){

	REP(i,n) d[i] = INF,vis[i] = false,pre[i] = 0;

	d[S] = 0; q.push(S); int u;

	while (!q.empty()){

		u = q.front(); q.pop();

		vis[u] = false;

		Redge(u) if (d[to = ed[k].to] > d[u] + 1 || (d[to] == d[u] + 1 && u < pre[to])){

			d[to] = d[u] + 1; pre[to] = u;

			if (!vis[to]) q.push(to),vis[to] = true;

		}

	}

	REP(i,n) if (i != S) p[i][S] = pre[i];

}

double dp(int u,int v){

	if (isc[u][v]) return f[u][v];

	isc[u][v] = true;

	if (u == v) return f[u][v] = 0;

	if (p[u][v] == v) return f[u][v] = 1;

	if (p[p[u][v]][v] == v) return f[u][v] = 1;

	int t = p[p[u][v]][v]; double ans = dp(t,v);

	Redge(v) ans += dp(t,ed[k].to);

	return f[u][v] = ans / (de[v] + 1) + 1;

}

int main(){

	n = read(); m = read(); cc = read(); kk = read();

	while (m--) build(read(),read());

	REP(i,n) spfa(i);

	printf("%.3lf\n",dp(cc,kk));

	return 0;

}