洛谷 P1784 数独[DFS/回溯]

To 洛谷.1784 数独类似题：CODEVS.4966 简单数独（4*4数独） CODEVS.2924 数独挑战）

题目描述

数独是根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫内的数字均含1-9，不重复。每一道合格的数独谜题都有且仅有唯一答案，推理方法也以此为基础，任何无解或多解的题目都是不合格的。

芬兰一位数学家号称设计出全球最难的“数独游戏”，并刊登在报纸上，让大家去挑战。

这位数学家说，他相信只有“智慧最顶尖”的人才有可能破解这个“数独之谜”。

据介绍，目前数独游戏的难度的等级有一道五级，一是入门等级，五则比较难。不过这位数学家说，他所设计的数独游戏难度等级是十一，可以说是所以数独游戏中，难度最高的等级他还表示，他目前还没遇到解不出来的数独游戏，因此他认为“最具挑战性”的数独游戏并没有出现。

输入输出格式

输入格式：

一个未填的数独

输出格式：

填好的数独

输入输出样例

输入样例#1： 复制

8 0 0 0 0 0 0 0 0
0 0 3 6 0 0 0 0 0
0 7 0 0 9 0 2 0 0
0 5 0 0 0 7 0 0 0
0 0 0 0 4 5 7 0 0
0 0 0 1 0 0 0 3 0
0 0 1 0 0 0 0 6 8
0 0 8 5 0 0 0 1 0
0 9 0 0 0 0 4 0 0

输出样例#1： 复制

8 1 2 7 5 3 6 4 9
9 4 3 6 8 2 1 7 5
6 7 5 4 9 1 2 8 3
1 5 4 2 3 7 8 9 6
3 6 9 8 4 5 7 2 1
2 8 7 1 6 9 5 3 4
5 2 1 9 7 4 3 6 8
4 3 8 5 2 6 9 1 7
7 9 6 3 1 8 4 5 2

[分析]:

用三个数组进行标记每行、每列、每个子网格已用的数字，用于剪枝

bool row[10][10];    //row[i][x]  标记在第i行中数字x是否出现了

bool col[10][10];    //col[j][y]  标记在第j列中数字y是否出现了

bool g[10][10];   //g[k][x] 标记在第k个3*3子格中数字z是否出现了

row 和 col的标记比较好处理，关键是找出g子网格的序号与 行i列j的关系

即要知道第i行j列的数字是属于哪个子网格的

首先我们假设子网格的序号如下编排：

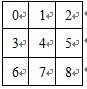
由于1<=i、j<=9，我们有： （其中“/”是C++中对整数的除法）

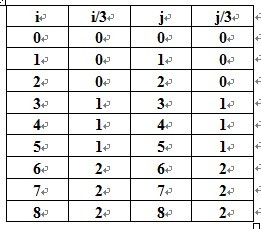
令a= i/3 , b= j/3  ，根据九宫格的 行列 与 子网格 的 关系，我们有:

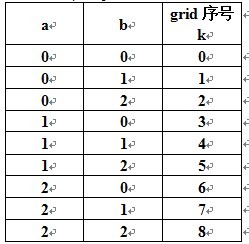
不难发现 3a+b=k

即 3*(i/3)+j/3=k

又我在程序中使用的数组下标为 1~9，grid编号也为1~9

因此上面的关系式可变形为 3*((i-1)/3)+(j-1)/3+1=k(第k个3*3子格中)

这样我们就能记录k个3*3子格中数字z是否出现了：

[代码]:

#include<cstdio>
#include<cstring>
#include<cstdlib>
int a[][];
bool h[][],l[][],g[][];//行，列，第几个格子
void print()//输出函数
{
    for(int i=;i<=;i++)
    {
        for(int j=;j<=;j++)
            printf("%d ",a[i][j]);
        printf("\n");
    }
   exit();
}

void dfs(int x,int y)//深搜
{
    if(a[x][y]!=)//9*9中不为零的数直接跳过
    {
        if(x==&&y==)
            print();  //搜索结束后输出
        if(y==)    //行到顶端后搜索列
            dfs(x+,);
        else    //搜索行
            dfs(x,y+);
    }
    if(a[x][y]==)//等于零时 待填数!
    {
        for(int i=;i<=;i++)
        {   //true未访问过
            if( h[x][i] && l[y][i] && g[(x-)/*+(y-)/+][i] )  //((i-1)/3)*3+(j-1)/3+1
            {
                a[x][y]=i;     //从1试到9
                h[x][i]=false;//此格被占 (行）
                l[y][i]=false;//同上（列）
                g[(x-)/*+(y-)/+][i]=false;//同上 （格子） 

                if(x==&&y==) //同a[x][y]!=0时
                    print();
                if(y==)
                    dfs(x+,);
                else
                    dfs(x,y+);

                a[x][y]=;  //当前格退出返回初状态
                h[x][i]=true;
                l[y][i]=true;
                g[(x-)/*+(y-)/+][i]=true;
            }
        }
    }
}

int main()
{
    memset(h,true,sizeof(h));
    memset(l,true,sizeof(l));
    memset(g,true,sizeof(g));
    for(int i=;i<=;i++)
    {
        for(int j=;j<=;j++)
        {
            scanf("%d",&a[i][j]);
            if(a[i][j]>)
            {
                h[i][a[i][j]]=false;//表示格子上有数
                l[j][a[i][j]]=false;//同上
                g[(i-)/*+(j-)/+][a[i][j]]=false;//同上
            }
        }
    }
    dfs(,);
    puts("\n");
    return ;
}

DFS

/*
根据二进制的思想，用二进制的第i位是0或1来表示数字是否已出现。
用 | 运算符进行标记，
用 ^ 运算符去标记，
用 & 运算符进行判重，
这样只需要一维的数组。
*/
#include<cstdio>
#define z(i) (1<<i)
#define g(x,y) (3*((x-1)/3)+(y-1)/3+1)
int h[],l[],s[],f[][],ok,sum=;
int read()
{
    int _=,___=;char __=getchar();
    while(__<''||__>''){if(__=='-')___=-;__=getchar();}
    while(__>=''&&__<=''){_=_*+__-'';__=getchar();}
    return _*___;
}
void out()
{
    for(int i=;i<=;i++)
      {
          for(int j=;j<=;j++)
            printf("%d ",f[i][j]);
          printf("\n");
      }
}
void dfs(int x,int y,int tot)
{
    while(f[x][y])
      {
          y++;
          if(y>) x++,y=;
      }
    for(int i=;i<=;i++)
      {
          if(h[x]&z(i)||l[y]&z(i)||s[g(x,y)]&z(i)) continue;   //用 & 运算符进行判重

          f[x][y]=i; h[x]|=z(i); l[y]|=z(i); s[g(x,y)]|=z(i); //用 | 运算符进行标记

          if(tot==sum) ok=;
          else dfs(x,y,tot+);
          if(ok) return ;

          f[x][y]=; h[x]^=z(i); l[y]^=z(i); s[g(x,y)]^=z(i); //用 ^ 运算符去标记
      }
}
int main()
{
    for(int i=;i<=;i++)
      for(int x,j=;j<=;j++)
        {
          f[i][j]=x=read();
          if(!x)continue;
          h[i]|=z(x); l[j]|=z(x); s[g(i,j)]|=z(x);
          sum--;
        }
    dfs(,,);
    out();
    return ;
}

状态压缩dfs