连续值的CART(分类回归树)原理和实现
上一篇我们学习和实现了CART(分类回归树),不过主要是针对离散值的分类实现,下面我们来看下连续值的cart分类树如何实现
思考连续值和离散值的不同之处:
二分子树的时候不同:离散值需要求出最优的两个组合,连续值需要找到一个合适的分割点把特征切分为前后两块
这里不考虑特征的减少问题
切分数据的不同:根据大于和小于等于切分数据集
def splitDataSet(dataSet, axis, value,threshold):
retDataSet = []
if threshold == 'lt':
for featVec in dataSet:
if featVec[axis] <= value:
retDataSet.append(featVec)
else:
for featVec in dataSet:
if featVec[axis] > value:
retDataSet.append(featVec) return retDataSet
选择最好特征的最好特征值
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
bestGiniGain = 1.0; bestFeature = -1;bsetValue=""
for i in range(numFeatures): #遍历特征
featList = [example[i] for example in dataSet]#得到特征列
uniqueVals = list(set(featList)) #从特征列获取该特征的特征值的set集合
uniqueVals.sort()
for value in uniqueVals:# 遍历所有的特征值
GiniGain = 0.0
# 左增益
left_subDataSet = splitDataSet(dataSet, i, value,'lt')
left_prob = len(left_subDataSet)/float(len(dataSet))
GiniGain += left_prob * calGini(left_subDataSet)
# print left_prob,calGini(left_subDataSet),
# 右增益
right_subDataSet = splitDataSet(dataSet, i, value,'gt')
right_prob = len(right_subDataSet)/float(len(dataSet))
GiniGain += right_prob * calGini(right_subDataSet)
# print right_prob,calGini(right_subDataSet),
# print GiniGain
if (GiniGain < bestGiniGain): #比较是否是最好的结果
bestGiniGain = GiniGain #记录最好的结果和最好的特征
bestFeature = i
bsetValue=value
return bestFeature,bsetValue
生成cart:总体上和离散值的差不多,主要差别在于分支的值要加上大于或者小于等于号
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
# print dataSet
if classList.count(classList[0]) == len(classList):
return classList[0]#所有的类别都一样,就不用再划分了
if len(dataSet) == 1: #如果没有继续可以划分的特征,就多数表决决定分支的类别
return majorityCnt(classList)
bestFeat,bsetValue = chooseBestFeatureToSplit(dataSet)
# print bestFeat,bsetValue,labels
bestFeatLabel = labels[bestFeat]
if bestFeat==-1:
return majorityCnt(classList)
myTree = {bestFeatLabel:{}}
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = list(set(featValues))
subLabels = labels[:]
# print bsetValue
myTree[bestFeatLabel][bestFeatLabel+'<='+str(round(float(bsetValue),3))] = createTree(splitDataSet(dataSet, bestFeat, bsetValue,'lt'),subLabels)
myTree[bestFeatLabel][bestFeatLabel+'>'+str(round(float(bsetValue),3))] = createTree(splitDataSet(dataSet, bestFeat, bsetValue,'gt'),subLabels)
return myTree
我们看下连续值的cart大概是什么样的(数据集是我们之前用的100个点的数据集)
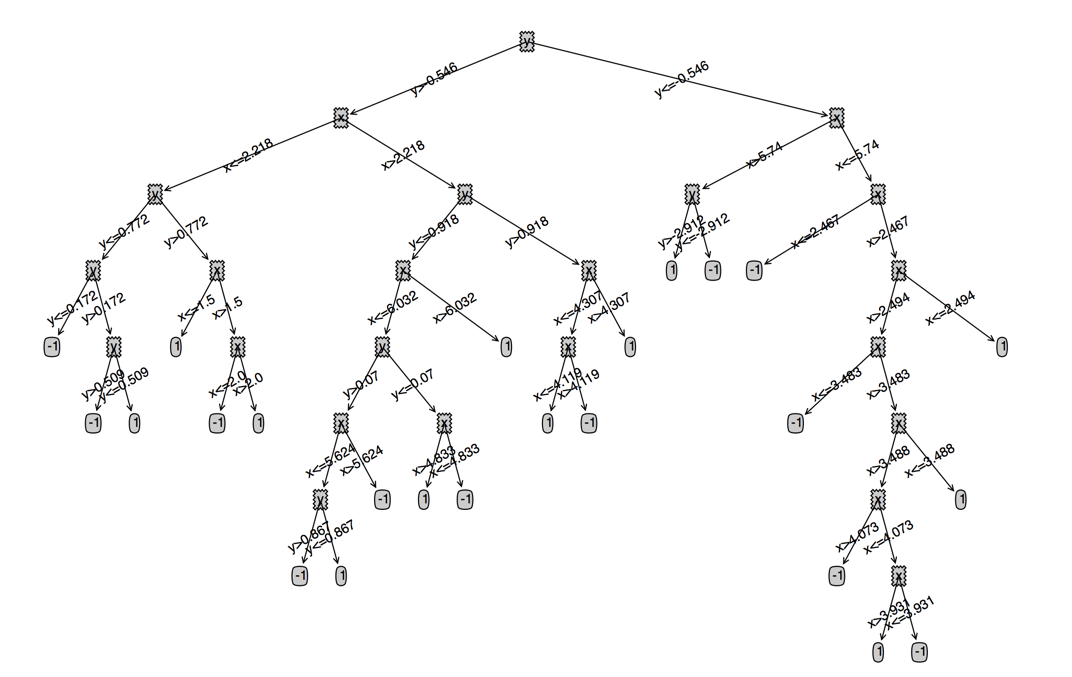
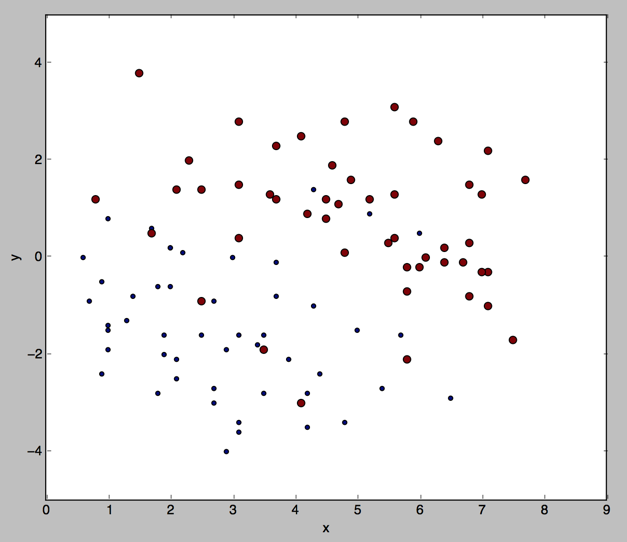
连续值的CART(分类回归树)原理和实现的更多相关文章
- 机器学习技法-决策树和CART分类回归树构建算法
课程地址:https://class.coursera.org/ntumltwo-002/lecture 重要!重要!重要~ 一.决策树(Decision Tree).口袋(Bagging),自适应增 ...
- 决策树的剪枝,分类回归树CART
决策树的剪枝 决策树为什么要剪枝?原因就是避免决策树“过拟合”样本.前面的算法生成的决策树非常的详细而庞大,每个属性都被详细地加以考虑,决策树的树叶节点所覆盖的训练样本都是“纯”的.因此用这个决策树来 ...
- 机器学习之分类回归树(python实现CART)
之前有文章介绍过决策树(ID3).简单回顾一下:ID3每次选取最佳特征来分割数据,这个最佳特征的判断原则是通过信息增益来实现的.按照某种特征切分数据后,该特征在以后切分数据集时就不再使用,因此存在切分 ...
- 利用CART算法建立分类回归树
常见的一种决策树算法是ID3,ID3的做法是每次选择当前最佳的特征来分割数据,并按照该特征所有可能取值来切分,也就是说,如果一个特征有四种取值,那么数据将被切分成4份,一旦按某特征切分后,该特征在之后 ...
- CART决策树(分类回归树)分析及应用建模
一.CART决策树模型概述(Classification And Regression Trees) 决策树是使用类似于一棵树的结构来表示类的划分,树的构建可以看成是变量(属性)选择的过程,内部节 ...
- 分类回归树(CART)
概要 本部分介绍 CART,是一种非常重要的机器学习算法. 基本原理 CART 全称为 Classification And Regression Trees,即分类回归树.顾名思义,该算法既 ...
- 秒懂机器学习---分类回归树CART
秒懂机器学习---分类回归树CART 一.总结 一句话总结: 用决策树来模拟分类和预测,那些人还真是聪明:其实也还好吧,都精通的话想一想,混一混就好了 用决策树模拟分类和预测的过程:就是对集合进行归类 ...
- 分类-回归树模型(CART)在R语言中的实现
分类-回归树模型(CART)在R语言中的实现 CART模型 ,即Classification And Regression Trees.它和一般回归分析类似,是用来对变量进行解释和预测的工具,也是数据 ...
- CART(分类回归树)
1.简单介绍 线性回归方法可以有效的拟合所有样本点(局部加权线性回归除外).当数据拥有众多特征并且特征之间关系十分复杂时,构建全局模型的想法一个是困难一个是笨拙.此外,实际中很多问题为非线性的,例如常 ...
随机推荐
- Eclipse Maven to create Struts2 Project
Follow the guide in this page: http://blog.csdn.net/topwqp/article/details/8882965 problem met : Des ...
- Android 组件系列-----Activity保存状态
本篇随笔将详细的讲解Activity保存状态的概念,也就是saving activity state. 一.Activity状态保持概念 保存Activity的状态是非常重要的,例如我们在玩一个游戏的 ...
- arcgis打开图层后右下角坐标小数点位数调整
打开arcmap,加载图层后,在其右下方会显示鼠标移动的点坐标,但是默认显示的小数点只有三位,如果是经纬度坐标,只有三位的话不够精确,因此想着能否改变其显示的精度,搜了半天,算是搜到了,但是过了一段时 ...
- 参数传递的四种形式----- URL,超链接,js,form表单
什么时候用GET, 查,删, 什么时候用POST,增,改 (特列:登陆用Post,因为不能让用户名和密码显示在URL上) 4种get传参方式 <html xmlns="http:/ ...
- BZOJ 2648: SJY摆棋子 kdtree
2648: SJY摆棋子 题目连接: http://www.lydsy.com/JudgeOnline/problem.php?id=2648 Description 这天,SJY显得无聊.在家自己玩 ...
- 小兔的棋盘(hdu2067)
小兔的棋盘 Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Subm ...
- 云服务器上安装配置Filezilla Server的坑!
1.Filezilla被动模式配置如下,需要使用比较大号的端口,用1024以内的不行! 2.相应的,IP筛选器放开TCP-50020端口.不是UDP! 3.可以正常访问了.GOOD! 4.注意,服务器 ...
- java利用透明的图片轮廓抠图
需要处理的图片: 1.png(空白区域为透明) 2.png 处理后的结果图片:result.png 代码如下: import java.awt.Graphics2D; import java.awt. ...
- GitLab 的 Developer 角色没有权限提交问题
"C:\Program Files\Git\bin\git.exe" push --recurse-submodules=check --progress "origin ...
- JavaScriptSerializer 中的匿名类型 转json
二:JavaScriptSerializer 中的匿名类型 这个类型我想大家都清楚,不过性能更高的方式应该是用JsonConvert吧,但这个不是本篇讨论的话题,我们重点来看看匿名类型的Json序列化 ...
