P2711 小行星 (最大流)

题目

P2711 小行星

解析

这道题挺巧妙的，乍一看是空间上的，无从下手，稍微转换一下就可以了。

看到题目，求消除这些行星的最少次数，就是求最小割，也就是求最大流，考虑怎样建图。

考虑当我们消去一个面上的所有点时，我们消去这个面后，这个面就不会再被消了，也就是只能被消一次，比如我们消去与\(\texttt{x=1}\)垂直的面上的点后，与\(\texttt{x=1}\)垂直的这个面就不会被再消一次，\(\texttt{y,z}\)同理。

但在这个面上的某些点（\(\texttt{x}\)相同，\(\texttt{y}\)，\(\texttt{z}\)不同的点）还会在另一些平面上，可能还会被再消。

直接连点的话会超时，我们考虑用点来代表面(例如\(\texttt{x}\)中的1号点就代表与\(\texttt{x=1}\)垂直的面)，三个面就可以确定一个点，所以我们让\(\texttt{x}\)与\(\texttt{y}\)与\(\texttt{z}\)相连，表示这个点。

我们这样建图

建立一个超级汇点\(\texttt{s}\)和超级源点\(\texttt{t}\)，\(\texttt{s}\)向所有\(\texttt{x}\)连边，\(\texttt{x}\)向\(\texttt{y}\)连边，\(\texttt{y}\)拆一下子点，拆完点出来向\(\texttt{z}\)连边，所有\(\texttt{z}\)向\(\texttt{t}\)连边。



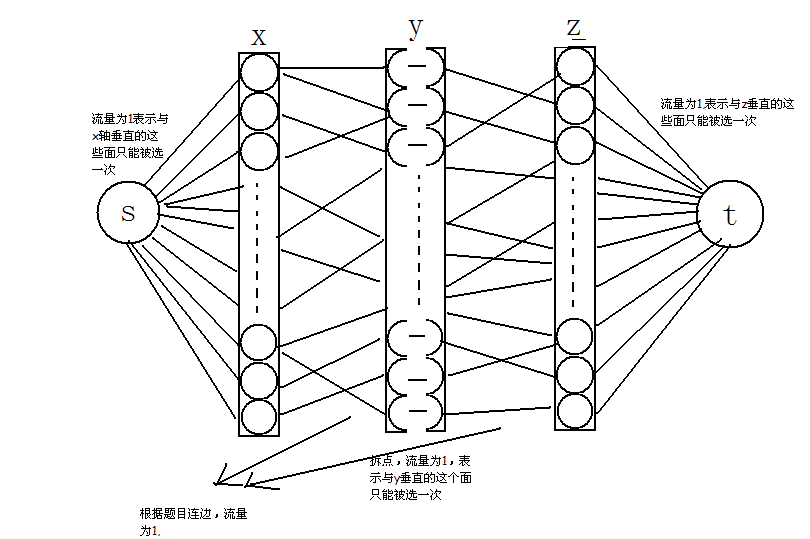
当我们某一条\(\texttt{s->x}\)的边流满时，就代表与\(\texttt{x}\)垂直的这个面被消掉了，\(\texttt{y->y'}\)流满时表示与\(\texttt{y}\)垂直的这个面被消了，\(\texttt{z->t}\)流满时表示与\(\texttt{z}\)垂直的这个面被消了，因为我们要求最小割，所以跑一遍最大流就行了。

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
const int INF = 0x3f3f3f3f;
int n, m, s, t, num = 1;
int head[N], cur[N], dep[N];
class node {
	public :
		int v, nx, w;
} e[N];

template<class T>inline void read(T &x) {
    x = 0; int f = 0; char ch = getchar();
    while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
    while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
    x = f ? -x : x;
    return ;
}

inline void add(int u, int v, int w) {
	e[++num].nx = head[u], e[num].v = v, e[num].w = w, head[u] = num;
	e[++num].nx = head[v], e[num].v = u, e[num].w = 0, head[v] = num;
}

queue<int>q;
bool bfs() {
	memset(dep, 0, sizeof dep);
	memcpy(cur, head, sizeof cur);
	dep[s] = 1;
	q.push(s);
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = head[u]; ~i; i = e[i].nx) {
			int v = e[i].v;
			if (!dep[v] && e[i].w) dep[v] = dep[u] + 1, q.push(v);
		}
	}
	return dep[t];
}

int dfs(int u, int flow) {
	if (u == t) return flow;
	int use = 0;
	for (int &i = cur[u]; ~i; i = e[i].nx) {
		int v = e[i].v;
		if (e[i].w && dep[v] == dep[u] + 1) {
			int di = dfs(v, min(flow, e[i].w));
			e[i].w -= di, e[i ^ 1].w += di;
			use += di, flow -= di;
			if (flow <= 0) break;
		}
	}
	return use;
}

int dinic() {
	int ans = 0;
	while (bfs()) ans += dfs(s, INF);
	return ans;
}

int main() {
	memset(head, -1, sizeof head);
	read(n), read(m);
	for (int i = 1, x, y, z; i <= n; ++i) read(x), read(y), read(z), add(x, y, z);
	s = 1, t = m;
	printf("%d\n", dinic());
}