使用穷举法结合numpy解决八皇后问题

一般说到八皇后问题，最先想到的就是回溯思想，而回溯思想往往是需要递归来实现的。

计算机很善长做重复的事情，所以递归正和它的胃口，而我们人脑更喜观平铺直叙的思维方式。当

我们看到递归时，总想把递归平铺展开，脑子里就会循环，一层一层往下调，然后再一层一层返回

试图想搞清楚计算机每一步都是怎么执行的，这样就很容易被绕进去。

我就是一个例子，当用递归解决归并或快速排序时，由于问题本身不是很复杂，递归代码还是比较简单能写出来的

但八皇后，我在网上看了相应的代码，总感觉还是似懂非懂，很容易就被绕了进去。

所以我尝试用穷举的方法解决八皇后的问题，

思路如下

• 穷举每一种摆法
• 对每一种摆法，转换成nunpy array
• 分别判断每一行，每一列，每个左下对角线，每个右下对角线是否满足需要

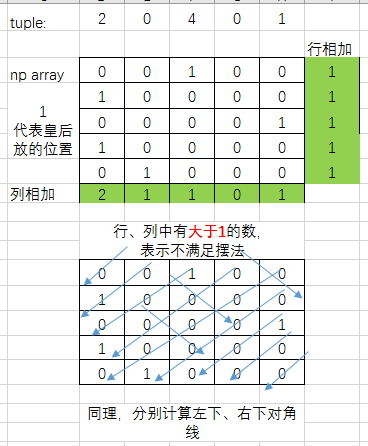
直接看代码：

import numpy as np
import itertools

BOARD_SIZE = 8
result = [0] * BOARD_SIZE   # 下标表示行，值表示列

# 将tuple 比如 (2,0,1) 转成numpy array:
#array([[0, 0, 1],
#       [1, 0, 0],
#       [0, 1, 0]])

def get_np_represent(result):
    x = np.zeros([len(result),len(result)])

    for i,v in enumerate(result):
        x[i, v] = 1
    return x

# 判断相应的行（横、纵、左下对角线、右下对角线）是否满足需要
def line_not_pass(np):
    return (np > 1).any()

# 获取左下对角线相加的数组
def left_diag_array(np_array):

    left_diag_array = [np.sum(np.diag(np.fliplr(np_array), d)) for d in range(len(np_array) - 1, -len(np_array), -1)]

    return np.array(left_diag_array)

# 获取右下对角线相加的数组
def right_diag_array(np_array):
    right_diag_array = [np.sum(np.diag(np_array, d)) for d in range(len(np_array) - 1, -len(np_array), -1)]
    return np.array(right_diag_array)

match_count = 0

# main
for arr in itertools.product(list(range(0,BOARD_SIZE)),repeat=BOARD_SIZE):

    np_array = get_np_represent(arr)

    row_array = np_array.sum(axis=1)
    if line_not_pass(row_array):
        continue
    col_array = np_array.sum(axis=0)
    if line_not_pass(col_array):
        continue

    if line_not_pass(left_diag_array(np_array)):
        continue

    if line_not_pass(right_diag_array(np_array)):
        continue

    match_count +=1

print("total count:",match_count)