谱聚类（Spectral clustering）（2）:NCut

作者：桂。

时间：2017-04-13  21:19:41

链接：http://www.cnblogs.com/xingshansi/p/6706400.html

声明：欢迎被转载，不过记得注明出处哦~

---

前言

本文为谱聚类的第二篇，主要梳理NCut算法，关于谱聚类的更多细节信息，可以参考之前的博文：

　　1）拉普拉斯矩阵（Laplace Matrix）与瑞利熵（Rayleigh quotient）

　　2）谱聚类之RatioCut算法

内容主要参考刘建平Pinard博客，更多细节可以参考该作者博文，本文最后给出代码实现，全文包括：

　　1）NCut原理

　　2）NCut算法实现

一、NCut原理

　　Ncut切图和RatioCut切图很类似，但是把Ratiocut的分母$|Ai|$换成$vol(A_i)$，由于子图样本的个数多并不一定权重就大，我们切图时基于权重也更合我们的目标，因此一般来说Ncut切图优于RatioCut切图。

$vol(A): = \sum\limits_{i \in A}d_i$

对应的，Ncut切图对指示向量h做了改进。注意到RatioCut切图的指示向量使用的是$\frac{1}{\sqrt{|A_j|}}$标示样本归属，而Ncut切图使用了子图权重$\frac{1}{\sqrt{vol(A_j)}}$来标示指示向量h，定义如下:

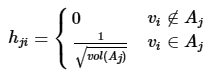
那么我们对于$h_i^TLh_i$有：

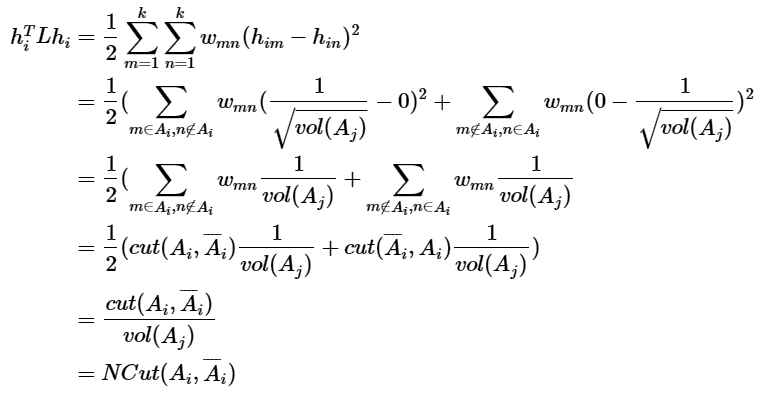
推导方式和RatioCut完全一致。也就是说，我们的优化目标仍然是

但是此时我们的$H^TH \neq I$而是$H^TDH = I$，推导如下：

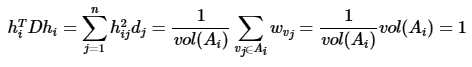
也就是说，此时我们的优化目标最终为：

这个就是泛化瑞利熵的求解问题，之前文章分析过。这里再次给出细节分析。

令$H = D^{-1/2}F$，则优化目标转化为：

至此已经完成了NCut的理论。

画蛇添足一下吧，注意到：

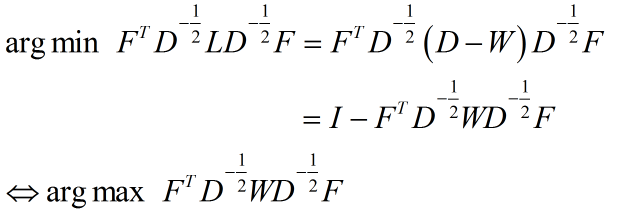
事实上，连拉普拉斯矩阵都懒得构造了。

二、NCut算法实现

首先给出算法步骤：

步骤一：求解邻接矩阵W和度矩阵D

步骤二：对${D^{ - \frac{1}{2}}}W{D^{ - \frac{1}{2}}}$进行特征值分解，并取K个最大特征值对应的特征向量（K为类别数目）

步骤三：将求解的K个特征向量（并分别归一化），构成新的矩阵，对该矩阵进行Kmeans处理

Kmeans得到的类别标签，就是原数据的类别标签，至此完成NCut聚类。

给出代码实现：

sigma2 = 0.01;
%%Step1: Calculate  matrixs
for i = 1:N
    for j =1:N
        W(i,j) = exp(-sqrt(sum((X(i,:)-X(j,:)).^2))/2/sigma2);
    end
end
W = W-diag(diag(W));% adjacency matrix
D = diag(sum(W)); %degree matrix
%%Step2:Eigenvalues decomposition
K = 3;
[Q,V] = eigs(D^(-1/2)*W*D^(-1/2),K);
%%Step3:New matrix Q
Q = Q./repmat(sqrt(diag(Q'*Q)'),N,1);
[idx,ctrs] = kmeans(Q,K);　

结果图：

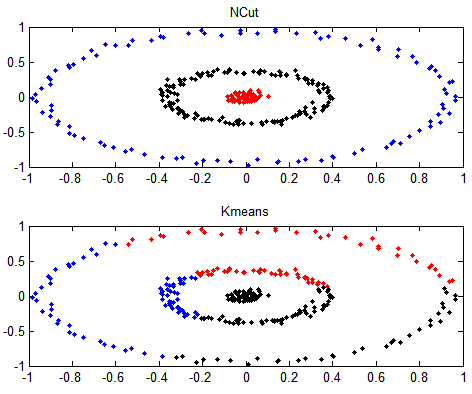
测试一下，按数据为3类进行谱聚类，可以看出来还是有效的，谱聚类中高斯权重涉及到$\sigma$如何取值，不过这里就不做进一步讨论了。

参考：

• http://www.cnblogs.com/pinard/p/6221564.html