BFS与DFS算法解析

1）前言

　　和树的遍历类似，图的遍历也是从图中某点出发，然后按照某种方法对图种所有顶点进行访问，且仅访问一次。

　　但是图的遍历相对树的遍历更为复杂，因为图中任意顶点都能与其他顶点相邻，所以在图的遍历中必须记录已经被访问的顶点，避免重复访问。

　　根据搜索路径不同，我们可以将遍历图的方法分为两种：广度优先搜索和深度优先搜索。

2）图的基本概念

　　1.无向图

　　　顶点对(u，v)是无序的，即（u，v）和（v，u）是同一条边。常用一对圆括号表示。

　　　　

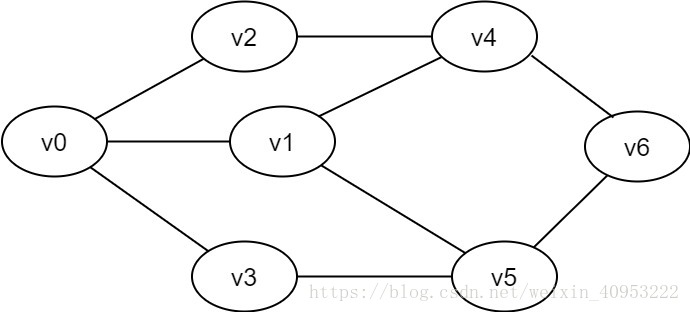
　　　　　　　　　　　　　　　　　　　　　　　　图2-1-1 无向图示例

　　顶点对<u,v>是有序的，它是指从顶点u到顶点 v的一条有向边。其中u是有向边的始点，v是有向边的终点。常用一对尖括号表示

　　

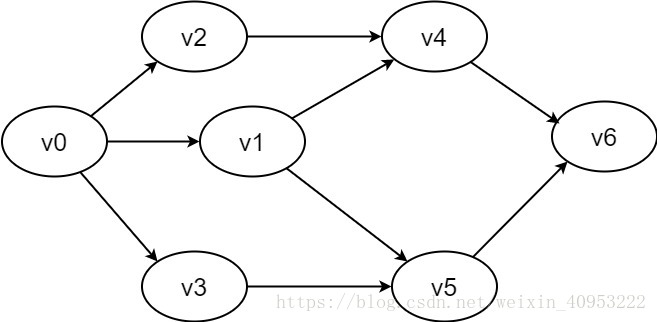
　　　　　　　　　　　　　　　　　　　　　　　　图2-1-2 有向图示例　　

　　2.权和网

　　图的每条边上可能存在具有某种含义的数值，称该数值为该边上的权。而这种带权的图被称为网。

　　3.连通图和非连通图

　　连通图：在无向图G中，从顶点v到顶点v'有路径，则称v和v'是联通的。若图中任意两顶点v、v'∈V，v和v'之间均联通，则称G是连通图。上述两图均为连通图。

　　非连通图：若无向图G中，存在v和v'之间不连通，则称G是非连通图。

　　　　

　　　　　　　　　　　　　　　　

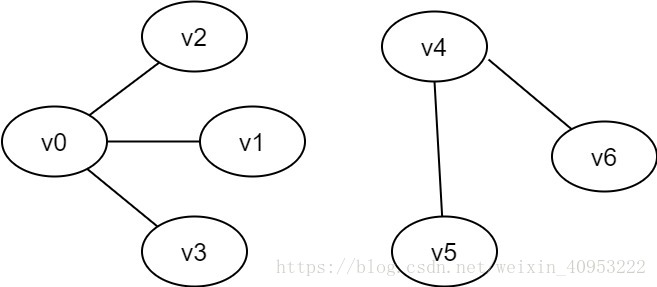
　　　　　　　　　　　　　　　　　　　　　　图2-3 非连通图示例

3）广度优先搜索

　　1.算法基本思路

　　广度优先搜索类似于树的层次遍历过程。它需要借助一个队列来实现。如图2-1-1所示，要想遍历从v0到v6的每一个顶点，我们可以设v0为第一层，v1、v2、v3为第二层，v4、v5为第三层，v6为第四层，再逐个遍历每一层的每个顶点。

　　具体过程如下：

　　　　1.准备工作：创建一个visited数组，用来记录已被访问过的顶点；创建一个队列，用来存放每一层的顶点；初始化图G。

　　　　2.从图中的v0开始访问，将的visited[v0]数组的值设置为true，同时将v0入队。

　　　　3.只要队列不空，则重复如下操作：

　　　　　　(1)队头顶点u出队。

　　　　　(2)依次检查u的所有邻接顶点w，若visited[w]的值为false，则访问w，并将visited[w]置为true，同时将w入队。