LR--用栈实现移进--归约分析(demo)

1.考虑文法

\(E->E+E\)

\(E->E*E\)

\(E->id\)

2.最右推导

不难看出，这个文法是而二义的，所以有多个最右推导

3.移进归约

用一个栈存文法符号，用输入缓存区保存要分析的输入串，用$标记栈底

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<stack>
using namespace std;
stack<string> stk, tmp;
string w;
bool flag = false;
int main(void) {
	cin >> w;	//输入串
	w += "$";	//加上标识符
	printf("----------|----------|----------\n");
	printf("    栈    |   输入   |    动作  \n");
	printf("----------|----------|----------\n");
	int now = 0;	//当前扫描字符位置
	while (!flag) {
		now = 0;
		if (stk.empty()) {	//如果一开始栈为空，直接移进符号
			stk.push("$");
			cout << "$         |";
			cout.setf(ios::right);	//设置字符对其方式
			cout.width(10);			//设置字符宽度
			cout << w;
			cout<< "|移进" << endl;
			printf("----------|----------|----------\n");
			string tt;
			if (w[now] == 'i') {	//移进符号为id
				tt = "id";
				now = 2;
			}
			else {					//移进符号不为id
				tt = w[now];
				now = 1;
			}
			stk.push(tt);			//将符号压入栈
			w = w.substr(now, w.size() - now);	//丢弃已扫描的字符
			continue;
		}
		while (!stk.empty()) {		//用两个栈来回倒，输出字符
			tmp.push(stk.top());
			stk.pop();
		}
		while (!tmp.empty()) {
			cout << tmp.top();
			stk.push(tmp.top());
			tmp.pop();
		}
		if (stk.top() == "id") {	//E-->id归约，优先级最高
			cout.width(10-stk.size());
			cout << "|";
			cout.setf(ios::right);	//设置字符对其方式
			cout.width(10);			//设置字符宽度
			cout << w;
			cout<< "|按E-->id进行归约" << endl;
			printf("----------|----------|----------\n");
			stk.pop();
			stk.push("E");
			continue;
		}
		if (w[now]=='$'&&stk.size() == 2 && stk.top() == "E") {		//接受状态
			flag = true;
			cout<< "        |         $|接受"<< endl;
			printf("----------|----------|----------\n");
			continue;
		}
		if (w[now]!='$') {		//移进字符
			string tp;
			if (w[now] == 'i') {
				tp = "id";
				now = 2;
			}
			else {
				tp = w[now];
				now = 1;
			}
			cout.width(11 - stk.size());
			cout << "|";
			cout.setf(ios::right);	//设置字符对其方式
			cout.width(10);			//设置字符宽度
			cout << w;
			cout<< "|移进" << endl;
			printf("----------|----------|----------\n");
			stk.push(tp);
			w = w.substr(now, w.size() - now);	//丢弃已扫描的字符
			continue;
		}
		if (w[now] == '$'  &&!flag) {	//E-->E+E或者E-->E*E归约
			string  tc;
			tc = stk.top();
			if (tc == "E")
				stk.pop();
			tc += stk.top();
			if (stk.top() != "E") {
				stk.pop();
				tc += stk.top();
				cout.setf(ios::right);	//设置字符对其方式
				cout.width(9- stk.size());//设置字符宽度
				cout << "|";
				cout << "         $|";
				cout << "按E-->"<<tc<<"归约" << endl;
				printf("----------|----------|----------\n");
				stk.pop();
				stk.push("E");
			}
		}
	}
	return 0;
}

4.Sample

输入

id*id+id

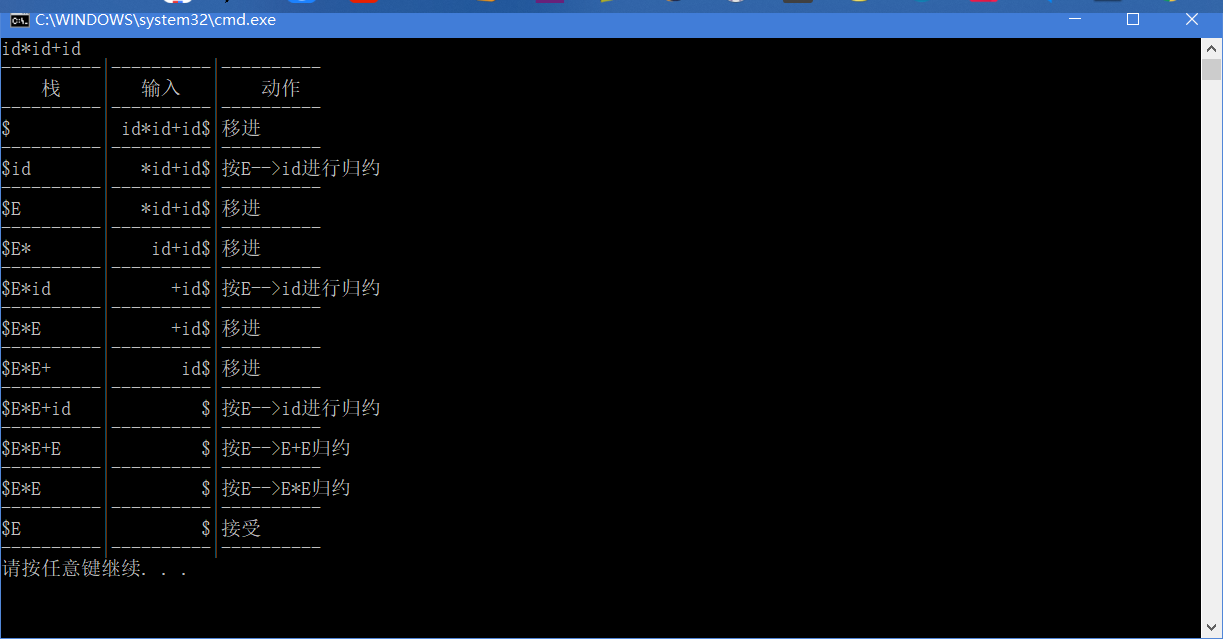
5.To be continued.