解魔方的机器人攻略17 – 魔方CFOP算法

由 动力老男孩 发表于 2010/01/03 17:38:09

本来我想把这个攻略做成一个NXT开发的教程，把传感器，电机，发声等部分都介绍一遍。不过现在看来有些同学很心急，希望早点看到“核心代码”，所以我提前把解魔方的算法写出来。其实魔方的算法网上有很多，只要你耐心并且有效的使用搜索引擎，会发现上个世纪就已经有人公布算法或源代码了，例如
算法：http://www.zunny.com/RUBIK.HTM
代码：http://tomas.rokicki.com/cubecontest/

不过我做第一版的时候，还是决定自己动手写算法。原因很简单：我玩魔方很多年了，把玩法转成算法也是我的目标之一。在写程序之前，我画了以下的几张草图：

魔方算法的草稿

话说曾经有位同事本打算和我一起做萝卜头的，看了这些草图以后，决定还是继续打游戏更靠谱。这不禁让我想起一首歌“1979年，那是一个春天，有一位老人在中国的南海边画了一个圈…” 这位老同志一定是资深软件架构师，改革开放这么宏伟的事情，画个圈就搞定了。
这样说来我这个草图是太复杂了，难怪把人吓跑了。今天特地又重画了些好看的图，以便大家理解。

魔方表示法
算法的第一个问题就是，怎么用数学方式描述一个魔方状态。我的做法是把魔方想象成一个纸盒子，沿边缝剪开铺平，就形成了六个面，我按照图里的顺序给它们编了号。
每个面又包含了9个颜色小方块，我也按照图中的顺序给它们编了号。

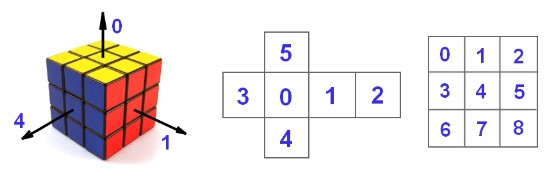
魔方的数组表示法

这样一来，立体的魔方就变成了一个 6*9 的数组。例如下面是一个普通的被打乱的魔方：

1. static String SideColors[] = {
2. "orgorwwoo",
3. "oyggbobrg",
4. "yyrgowwbw",
5. "yrybgybbo",
6. "gwwyybror",
7. "bgrwwrbgy"

static String SideColors[] = {
  "orgorwwoo",
  "oyggbobrg",
  "yyrgowwbw",
  "yrybgybbo",
  "gwwyybror",
  "bgrwwrbgy"

魔方坐标系：
啥？怎么又有坐标系，刚才的表示法不就完全描述了一个魔方吗？没错，但是咱们的萝卜头每次只能旋转魔方的最下面一层，假设我们需要旋转最上面一层，就必须先把它翻到下面。
请注意在翻跟头的过程中，魔方本身并没有变化，只是坐标系变了。所以还需要一个坐标系来对应萝卜头的空间：

魔方坐标系

状态变化：
正如刚才所说，魔方在萝卜头的数字世界里有两种变化形式：1，翻跟头；2，旋转某一面。
每次状态变化都会造成SideColors数组发生变化，这种转换用最简单的查表法就可以搞定：

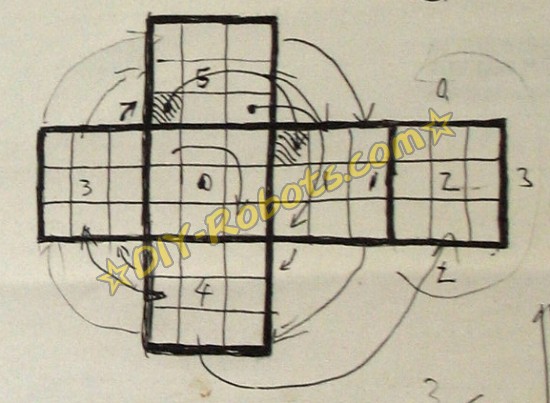
坐标变化的大概示意图，坐标变化没啥难度，主要看耐心

例如，这是一段旋转底面后状态转换的代码：

1. public static void RotateBottomSide(boolean ClockWise) throws Exception
2. {
3. int temp=0;
4. int i;
5. CopyMatrics(2,6,ClockWise?2:1); //Bottom ClockWise = Top Anti-ClockWise
6. CopyMatrics(6,2,0);
7. if(ClockWise)
8. {
9. for(i=0;i<3;i++)
10. {
11. temp=Sides[5][0][i];
12. Sides[5][0][i]=Sides[3][2-i][0];
13. Sides[3][2-i][0]=Sides[4][2][2-i];
14. Sides[4][2][2-i]=Sides[1][i][2];
15. Sides[1][i][2]=temp;
16. }
17. }
18. else
19. {
20. for(i=0;i<3;i++)
21. {
22. temp=Sides[5][0][i];
23. Sides[5][0][i]=Sides[1][i][2];
24. Sides[1][i][2]=Sides[4][2][2-i];
25. Sides[4][2][2-i]=Sides[3][2-i][0];
26. Sides[3][2-i][0]=temp;
27. }
28. }
29. }

public static void RotateBottomSide(boolean ClockWise) throws Exception
{
 int temp=0;
 int i;

 CopyMatrics(2,6,ClockWise?2:1); //Bottom ClockWise = Top Anti-ClockWise
 CopyMatrics(6,2,0);
 if(ClockWise)
 {
  for(i=0;i<3;i++)
  {
   temp=Sides[5][0][i];
   Sides[5][0][i]=Sides[3][2-i][0];
   Sides[3][2-i][0]=Sides[4][2][2-i];
   Sides[4][2][2-i]=Sides[1][i][2];
   Sides[1][i][2]=temp;
  }
 }
 else
 {
  for(i=0;i<3;i++)
  {
   temp=Sides[5][0][i];
   Sides[5][0][i]=Sides[1][i][2];
   Sides[1][i][2]=Sides[4][2][2-i];
   Sides[4][2][2-i]=Sides[3][2-i][0];
   Sides[3][2-i][0]=temp;
  }
 }
}

CFOP解法：
这是由一位叫Jessica Fridrich女士发明的一种速解法，是目前世界上最流行的方块解法。
CROSS：字面上的意思为“十字”，是Fridrich Method中的第一步骤。
F2L：是“First 2 Layer”的缩写，意思为“一、二层”，是Fridrich Method中的第二步骤。
OLL：是“Orientation of Last Layer”的缩写，意思为“最后一层的角块排序”，这是Fridrich Method中的第三个步骤。
PLL：是“Permutation of Last Layer”的缩写，意思为“最后一层的排序”，这是Fridrich Method中的第四步骤。
CFOP：是Fridrich Method的的别称，就是四个步骤“Cross、F2L、OLL、PLL”原文的第一个字母合起来而成的。

上面这些文字比较费解，看下面的图就比较清楚了：

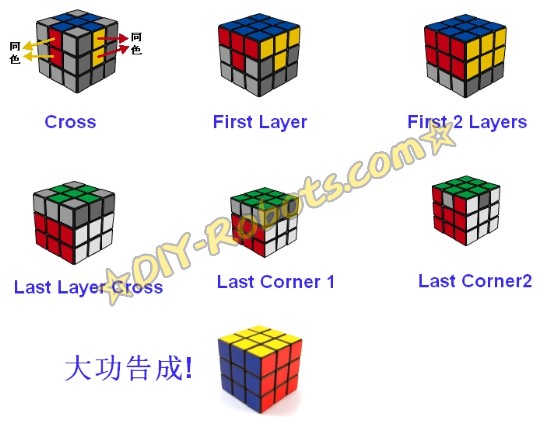
魔方的CFOP入门解法

或者你可以去魔方小站或者魔方吧看更详细的教程。

CFOP解法的实现：
这一部分比较繁琐，输入玩法公式的输入，按照上面的步骤实现以下函数：

1. TopCross();
2. TopCorner();
3. SecondLayer();
4. BottomCross();
5. BottomCorner();
6. ThirdLayerCorner();
7. ThirdLayerCornerSnap();
8. ThirdLayerBorderSnap();

TopCross();
TopCorner();
SecondLayer();
BottomCross();
BottomCorner();
ThirdLayerCorner();
ThirdLayerCornerSnap();
ThirdLayerBorderSnap();

CFOP算法的源代码可以点这里下载
通过这个CFOP算法，萝卜头完成了第一版：http://v.youku.com/v_show/id_XNDcwMDQ3NDQ=.html

这个算法的最大问题就是步骤太多，一般来说要120步左右，平均时间12分钟，大多数观众等不到转完就睡着了……
因为这个原因，我改用了一个更快的算法。写博客真是挺累啊，这个算法下次再介绍，心急的同学请看下面这个链接：
http://tomas.rokicki.com/cubecontest/ 点最上面的Winners，我用的是第二名的算法。