AI之旅（1）：出发前的热身运动

前置知识

  无

知识地图

自学就像在海中游泳

  当初为什么会想要了解机器学习呢，应该只是纯粹的好奇心吧。AI似乎无处不在，又无迹可循。为什么一个程序能在围棋的领域战胜人类，程序真的有那么聪明吗？如果掌握机器学习，就能创造属于自己的AI吗？

  怀着这样的好奇心，开始了在机器学习领域的探索。学习的第一步是从《吴恩达机器学习》公开课开始的，不可否认对于一个初学者而言，这始终是最好的入门课程。

  同样的知识也有不同的学法，比如一个公式摆在面前，浅一点的学法是直接把它背下来便于应用。深一点的学法是探究公式的原理和推导过程。不同的人倾向不同的学法。

  当选择了第二种学法后，“为什么...”这个概念开始不停涌现。当想要掌握每一个知识点时，立刻感觉困难重重。如同在海面上游泳试图深潜，巨大的阻力扑面而来。

学习中遇到的第一个问题

  学习的过程总是磕磕碰碰的，一会儿这里不懂，一会儿那里不懂。等到补上了相关知识回头看时，才会恍然大悟，啊，原来在这么简单的地方浪费了这么多的时间。

  单位时间效率低，这是学习中遇到的第一个问题。为什么会浪费这么多的时间呢，一方面是花费时间在网络上搜索信息，一方面是花费时间弥补缺失的前置知识。

  弥补缺失的知识应该不能算浪费时间，但是为了搜索信息而耗费大量的时间，就有些难以忍受了。除了锻炼一下搜索信息的能力外似乎没有什么益处。

学习中遇到的第二个问题

  学习的过程就是不断接触和认识新事物的过程。具体在机器学习中，这些新事物就是一种种算法。一种算法了解完之后，总是处于似懂非懂的状态，想要具体实现时不知从何下手。

  缺少直观上的认识，这是学习中遇到的第二问题。为什么会缺少直观上的认识呢，一方面是因为无法看见算法之间的联系，一方面是缺少一个简单易懂的例子。

  以上种种都是学习中可能会遇到的困难，不断克服困难固然会提升解决问题的能力，同时也消磨着学习的热情。如果同时出现了太多的困难，很容易就有放弃的念头。

  有没有更加平滑的学习曲线？

换一种形式来学

  写这些文章的目的，主要是为了把这磕磕碰碰的入门之旅记录下来。同时也在思考一个问题，有没有一种方式能够帮助更多的人用更经济的方法入门。

  设置前置知识：理解一个知识点需要的最低限度的前置知识，这里仅对前置知识做简要介绍。

  描绘知识地图：在已掌握和未掌握的知识点间建立联系，使得对于知识体系有个全局上的认识。

  构造最小模型：使用能够呈现算法本质的最小规模的例子，能够简洁直观地理解算法的本质。

从方程到矩阵

  下一篇要介绍的第一种算法是线性回归，现在开始为理解线性回归做一些准备工作。

  方程对于我们而言并不陌生，有几个方程组就能解几个未知数：

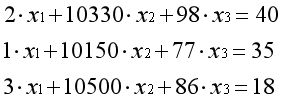
  仔细观察方程组会发现每一列的未知数是相同的：

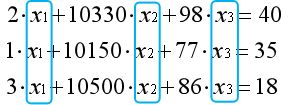
  如果把参数视为三维空间中的向量，方程可以表示为向量的线性组合：

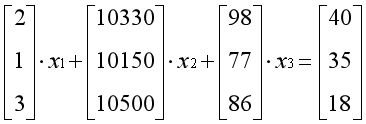
  如果把未知数也视为一个向量，方程也可以表示为矩阵和向量的乘积：

  那么下一个问题是，如果方程组的数量多于未知数的数量时该怎么解方程呢？这种情况可以用线性回归算法来处理。

  如果对向量和空间没有直观的认识，推荐观看《麻省理工公开课：线性代数》，这里面涉及的许多数学知识在后续中都会用得到。

Octave的使用

  动手实践会加深理解，把代码敲出来是很好的理解算法的途径。Octave是一款适用于数值计算的开源软件，相比于其他软件，它的优点是代码非常简洁。本文中的代码基于Octave实现。

  小任务：下载并安装Octave。

  网络上有很多介绍Octave如何使用的文章和视频，这里不再赘述，只讲以下几点，重点是要掌握通过帮助文档来学习调用函数的能力。

  1，向量的表示

  2，矩阵的表示

  3，画一幅图

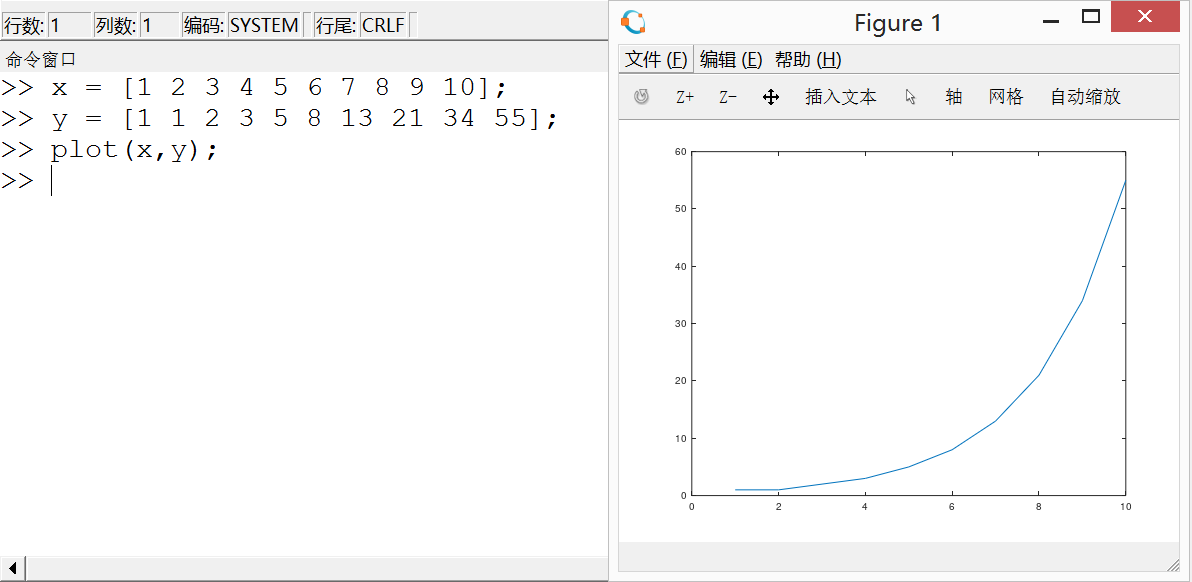
  4，实现一个for循环

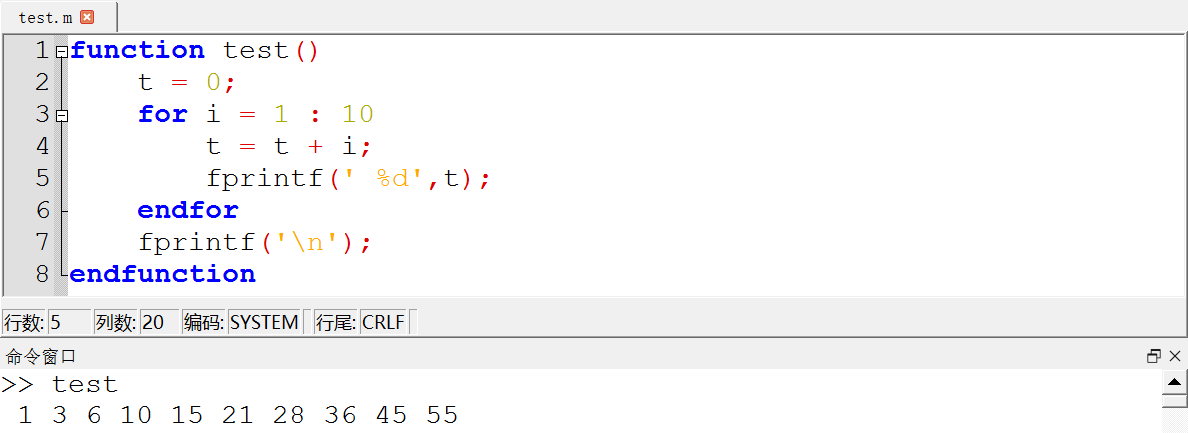
  5，看到不会的命令时怎么办？

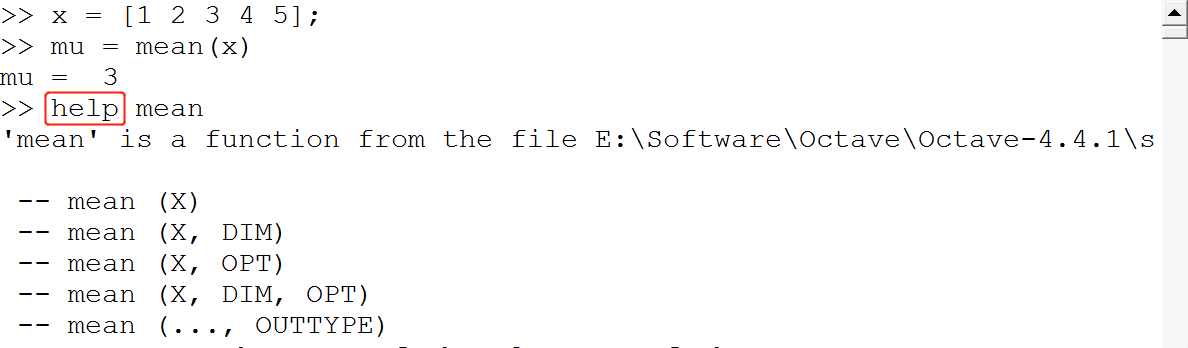
  6，英语不好怎么办？

https://ww2.mathworks.cn/help

结语

  至此我们已经具备了能够实现线性回归算法的技术水平了，是不是很惊讶？在下一篇中我们将使用类似的例子，对线性回归的原理进行讲解。让我们开始探索之旅，走起！