TSP（Traveling Salesman Problem）-----浅谈旅行商问题（动态规划,回溯实现）

　　1.什么是TSP问题

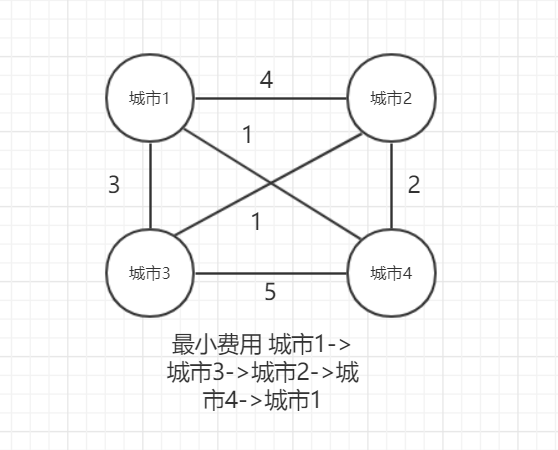
　　一个售货员必须访问n个城市，这n个城市是一个完全图，售货员需要恰好访问所有城市的一次，并且回到最终的城市。

　　城市于城市之间有一个旅行费用，售货员希望旅行费用之和最少。

　　完全图：完全图是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。

　　

　　2.TSP问题前提

　　　　回朔法：把所有的解列出来，形成一棵树，利用剪枝深度优先进行遍历，遍历的过程记录和寻找最优解。（剪枝就是把一条再深搜下去也不是最优解的分支剪去）。

　　　　动态规划：把一个大问题拆分成小问题，把小问题的最优结果通过表保留，在新问题需要用到的时候可以直接获取。

　　　　PS：下面的图，文字中出现1，2，3，4分别表示城市1，城市2，城市3，城市4

　　3.回朔法实现TSP问题

　　　　上面提到回朔法就是把所有的解列出来，形成一棵树，上面的例子形成的树如下：我们假设城市1为起点

　　　　

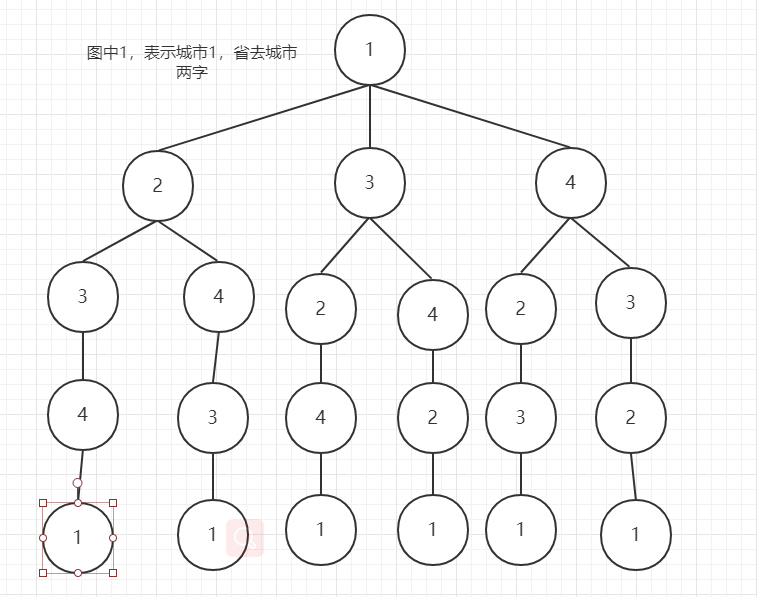
　　　　上面介绍回溯法就是把所有解列出来，然后剪枝深搜。那么我们需要解决的就是剪枝深搜了。剪枝深搜中最麻烦的就是找到何时剪枝的条件了。

　　　　首先我们假设不知道剪枝条件，先模拟深搜跑一遍。

　　　　

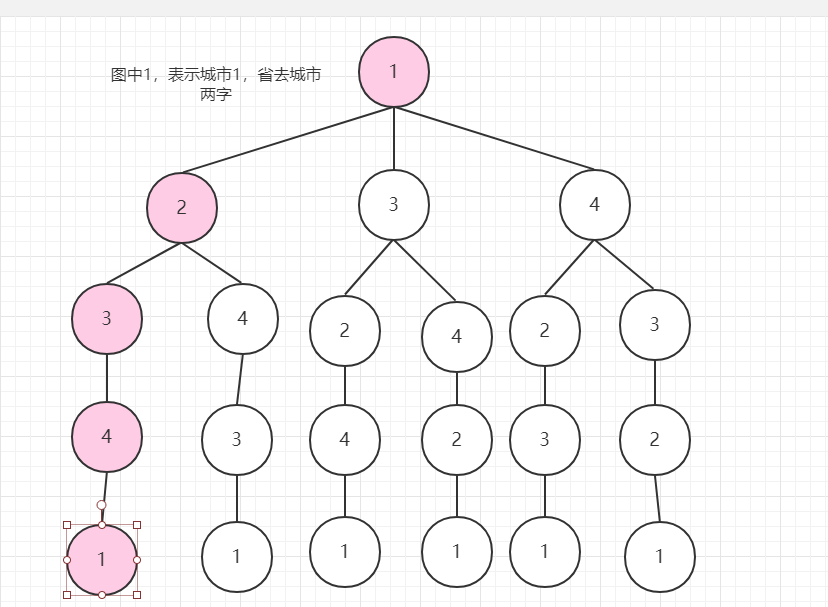
　　　　　从1深搜到4回到1，花费11，记录这个数值。接下来回溯，继续深搜。一步一步深搜的时候，遇到了一个特殊的时候：

　　　　

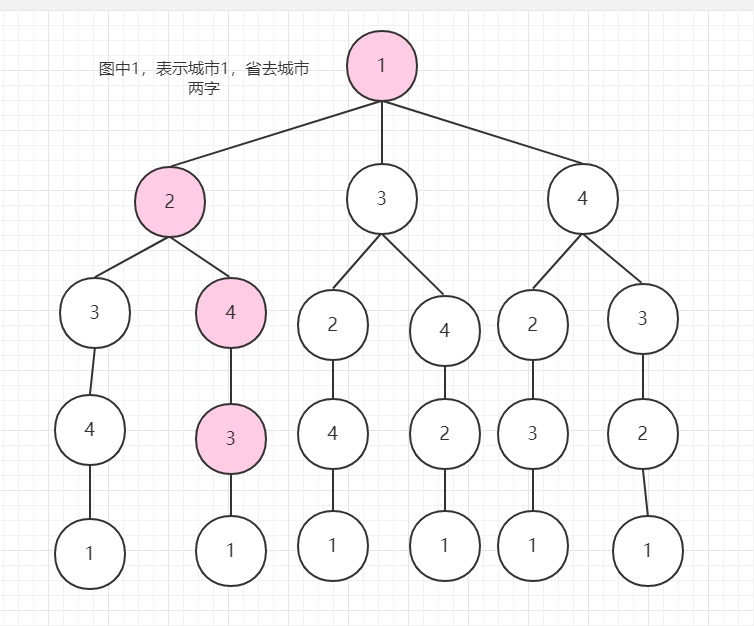
　　　　还记得我们之前记录的最短花费为11吗，1->2->4->3 花费已经11了，3回到1，还需要进行花费，不管花费多少，反正已经比我之前找出来的要大了，那这个时候我再深搜下去就没什么意义了，所以可以进行剪枝。我不继续找了，直接回溯。

　　　　所以剪枝条件出来了： 走下一步的距离 + 之前已经走过的距离的总和 >之前算出的最短路径 。

　　　　4.动态规划实现TSP

　　　　　　上面介绍了动态规划就是把大问题分解成小问题。我们现在的大问题是从1 经过2，3，4 回到1花费最少，那么我们把他分解一下。

　　　　　　我们从1出发有三种方案

　　　　　　

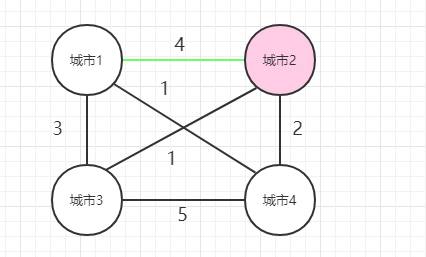
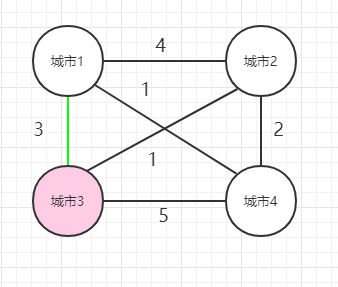
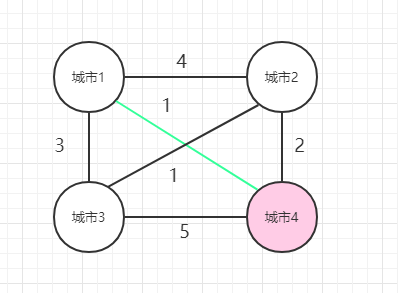
　　　　1、 从1出发，到2，然后再从2出发，经过[3,4]这几个城市，然后回到1，使得花费最少。

　　　　 2、 从1出发，到3，然后再从3出发，经过[2,4]这几个城市，然后回到1，使得花费最少。

　　　　 3、 从1出发，到4，然后再从4出发，经过[2,3]这几个城市，然后回到1，使得花费最少。

　　　　上面也提到了最优结果通过表来保留：设置一个二维的动态规划表dp , dp[1]{2，3，4}表示从1号城市出发，经过2，3，4 回到1花费最少。　　　　

　　　　要求上面三个方案的最小值意味：（D12表示1到2的距离，其他同理）

　　　　dp[1] [{2,3,4}] =  min{ D12+dp[2]{3,4} ，D13+dp[3]{2,4} ， D14+dp[4]{2,3}}　　　　　　

　　　　由于D12，D13，D14是已知的，那么我们现在的目的就是求dp[2]{3,4}，dp[3]{2,4}，dp[4]{2,3}，

　　　　照猫画虎，我们可以列出：（这里只列出dp[2]{3,4} ，其他两个类似）

　　　　dp[2]{3,4} = min{ D23+dp[3]{4} ，D24+dp[4][3}}

　　　　dp[3]{4}]= D43+dp[4]{}

　　　　dp[4]{}=D41

　　　　那么经过慢慢的分解，我们知道了我们已知了从4到1的最小花费，那么就可以推出从3出发经过4回到1的花费。。。。。。。从而推出我们所要求的最优解。

　　　　

5.时间复杂度分析

　　回溯法：

　　动态规划法：