【bfs】麻将游戏

题目

来自：yinzm的blog

在一种"麻将"游戏中，游戏是在一个有W＊H格子的矩形平板上进行的。每个格子可以放置一个麻将牌，也可以不放（如图所示）。玩家的目标是将平板上的所有可通过一条路径相连的两张相同的麻将牌，从平板上移去。最后如果能将所有牌移出平板，则算过关。

　　这个游戏中的一个关键问题是：两张牌之间是否可以被一条路径所连接，该路径满足以下两个特性：

　　1. 它由若干条线段组成，每条线段要么是水平方向，要么是垂直方向。

　　2. 这条路径不能横穿任何一个麻将牌 (但允许路径暂时离开平板)。

　　这是一个例子：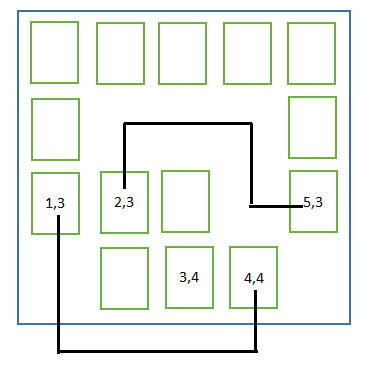　　　　　

　　在（1，3）的牌和在(4, 4)的牌可以被连接。(2, 3)和(3, 4)不能被连接。

　　你的任务是编一个程序，检测两张牌是否能被一条符合以上规定的路径所连接。

输入

第一行有两个整数w,h(1<=w，h<=75)，表示平板的宽和高。接下来h行描述平板信息，每行包含w个字符，如果某格子有一张牌，则这个格子上有个'X'，否则是一个空格。平板上最左上角格子的坐标为(1，1)，最右下角格子的坐标为(w,h)。接下来的若干行，每行有四个数x1, y1, x2, y2 ，且满足1<=x1,x2<=w,1<=y1,y2<=h，表示两张牌的坐标（这两张牌的坐标总是不同的）。如果出现连续四个0，则表示输入结束。

输出

对于每一对牌输出占一行，为连接这一对牌的路径最少包含的线段数。如果不存在路径则输出0。

样例输入

XXXXX
X   X
XXX X
 XXX 

样例输出

[思路]：用bfs求解注意外围一圈可以扩展，路径线段数就是最小转弯数+1

#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
,,,-};
,,-,};
struct point {
    int x,y,turn;
} _begin,_end,p;
queue<point> q;
][];
][];
int fun();
int main() {
    int w,h,i,j,bx,by,zx,zy;
    char ch;
    scanf("%d%d",&w,&h);
    getchar();
    n=h;
    m=w;
    ; i<=n+; i++) {
        a[i][]=;
        a[i][m+]=;
    }
    ; j<=m+; j++) {
        a[][j]=;
        a[n+][j]=;
    }
    ; i<=n; i++) {
        ; j<=m; j++) {
            ch=getchar();
            ;
            ;
        }
        getchar();
    }
    n++;
    m++;
    while(scanf("%d%d%d%d",&bx,&by,&zx,&zy)!=EOF) {
        &&zx==&&by==&&zy==)
        break;
        else {
            _begin.x=by;
            _begin.y=bx;
            _end.x=zy;
            _end.y=zx;
            a[zy][zx]=;
            fun();
            a[zy][zx]=;
        }
    }

    ;
}
int fun() {
    memset(visit,,sizeof(visit));
    while(!q.empty()) q.pop();
    q.push(_begin);
    q.front().turn=;
    while(!q.empty()) {
        ; i<; i++) {
            p.x=q.front().x+dx[i];
            p.y=q.front().y+dy[i];
            &&p.x<=n&&p.y>=&&p.y<=m&&!a[p.x][p.y]) {
                if(!visit[p.x][p.y]) {
                    if(p.x==_end.x&&p.y==_end.y) {
                        printf();
                        ;
                    }
                    visit[p.x][p.y]=;
                    p.turn=q.front().turn+;
                    q.push(p);
                }
                p.x+=dx[i];
                p.y+=dy[i];
            }
        }
        q.pop();
    }
    printf("0\n");
}