【BZOJ1502】【NOI2005】月下柠檬树

Portal

　　

　　传送门

　　

　　

　　

Solution

　　

　　显然的是，每一个圆的影子，就是从树上的圆按光线方向平移至地面的圆。至于两个圆之间的连接部分，则是每两个在树上相邻的圆的，对应的影子圆的，公切线围起来的部分，如下图所示

　　



　　

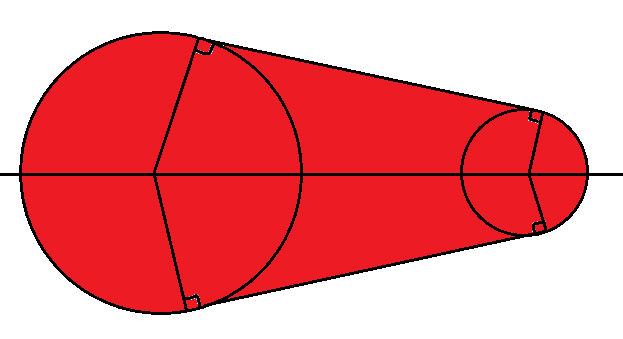
　　所以我们现在要求每两个在原树上相邻的圆的影子圆构成的图形的并。只看\(x\)轴上半部分，可以把它想象成一个函数，求单点值是\(O(n)\)的，我们不妨用辛普森积分来解决......

　　

　　相邻圆的公切线和x轴的夹角是可以求出来的，然后就能解出公切线的解析式，以及有效范围。注意这些东西要预处理！千万不要放在求值函数里面。\(EPS\)大约设置到\(10^{-7}\)才不会出错，效率也相对比较高。

　　

　　

　　

Code

　　

#include <cstdio>
#include <cmath>
using namespace std;
const int N=505;
const double EPS=1e-7,INF=1e10,PI=3.14159265358979323846;
int n,sum;
double alpha,h[N],p[N],r[N];
double k[N],b[N],lx[N],rx[N];
bool exist[N];
inline double max(double x,double y){return x>y?x:y;}
inline double min(double x,double y){return x<y?x:y;}
inline void swap(int &x,int &y){x^=y^=x^=y;}
inline bool in(int a,int b){
	if(r[a]>r[b]) swap(a,b);
	return p[a]+r[a]-EPS<=p[b]+r[b]&&p[a]-r[a]+EPS>=p[b]-r[b];
}
double calc(int a,int b,double &k,double &bb,double &xl,double &xr){
	if(p[a]>p[b]) swap(a,b);
	double beta=asin((r[b]-r[a])/(p[b]-p[a]));
	k=tan(beta);
	double tx;
	if(r[a]>=r[b]){
		beta=-beta;
		tx=p[b]+r[b]/sin(beta);
		bb=-k*tx;
		xr=tx-(cos(beta)*(r[b]/tan(beta)));
		xl=tx-(cos(beta)*(r[a]/tan(beta)));
	}
	else{
		tx=p[a]-r[a]/sin(beta);
		bb=-k*tx;
		xl=tx+(cos(beta)*(r[a]/tan(beta)));
		xr=tx+(cos(beta)*(r[b]/tan(beta)));
	}
}
double f(double x){
	double res=0;
	for(int i=1;i<=n;i++)
		if(fabs(x-p[i])<=r[i])
			res=max(res,sqrt(r[i]*r[i]-fabs(x-p[i])*fabs(x-p[i])));
	for(int i=1;i<n;i++)
		if(exist[i])
			if(lx[i]<=x+EPS&&x-EPS<=rx[i])
				res=max(res,k[i]*x+b[i]);
	return res;
}
double simpson(double l,double r){
	double mid=(l+r)*0.5;
	return (f(l)+4*f(mid)+f(r))*(r-l)/6;
}
double solve(double l,double r){
	double mid=(l+r)/2,lmid=(l+mid)/2,rmid=(mid+r)/2;
	double val=simpson(l,r);
	if(fabs(val-(simpson(l,mid)+simpson(mid,r)))<EPS) return val;
	return solve(l,mid)+solve(mid,r);
}
int main(){
	scanf("%d%lf",&n,&alpha);
	n++;
	for(int i=1;i<=n;i++){
		scanf("%lf",h+i);
		h[i]+=h[i-1];
		p[i]=h[i]/tan(alpha);
	}
	for(int i=1;i<n;i++) scanf("%lf",r+i);
	double xl=INF,xr=-INF;
	for(int i=1;i<=n;i++){
		xl=min(xl,p[i]-r[i]);
		xr=max(xr,p[i]+r[i]);
	}
	for(int i=1;i<n;i++){
		exist[i]=!in(i,i+1);
		if(exist[i])
			calc(i,i+1,k[i],b[i],lx[i],rx[i]);
	}
	printf("%.2lf\n",solve(xl,xr)*2);
	return 0;
}