2018.09.27 bzoj2510: 弱题（概率dp+循环矩阵优化）

传送门

简单概率dp。

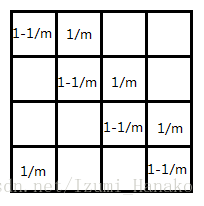
显然每次转移的式子可以用一个矩阵表示出来：



这个是循环矩阵。

因此只用维护第一行快速幂一波就行了。

代码：

#include<bits/stdc++.h>
#define N 1005
using namespace std;
int n,m,K,a[N];
double b[N];
struct Matrix{double val[N];}ans,tmp;
inline Matrix operator*(Matrix a,Matrix b){
	Matrix c;
	memset(c.val,0,sizeof(c.val));
	for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)c.val[(i+j-2)%n+1]+=a.val[i]*b.val[j];
	return c;
}
int main(){
	scanf("%d%d%d",&n,&m,&K);
	for(int i=1;i<=n;++i)scanf("%d",&a[i]);
	tmp.val[1]=1-1.0/m,tmp.val[2]=1.0/m,ans.val[1]=1;
	while(K){
		if(K&1)ans=ans*tmp;
		tmp=tmp*tmp,K>>=1;
	}
	for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)b[(i+j-2)%n+1]+=a[i]*ans.val[j];
	for(int i=1;i<=n;++i)printf("%.3lf\n",b[i]);
	return 0;
}