HDU 3435 A new Graph Game（最小费用最大流）&HDU 3488

A new Graph Game

Time Limit: 8000/4000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 1849    Accepted Submission(s): 802

Problem Description

An undirected graph is a graph in which the nodes are connected by undirected arcs. An undirected arc is an edge that has no arrow. Both ends of an undirected arc are equivalent--there is no head or tail. Therefore, we represent an
edge in an undirected graph as a set rather than an ordered pair.

Now given an undirected graph, you could delete any number of edges as you wish. Then you will get one or more connected sub graph from the original one (Any of them should have more than one vertex).

You goal is to make all the connected sub graphs exist the Hamiltonian circuit after the delete operation. What’s more, you want to know the minimum sum of all the weight of the edges on the “Hamiltonian circuit” of all the connected sub graphs (Only one “Hamiltonian
circuit” will be calculated in one connected sub graph! That is to say if there exist more than one “Hamiltonian circuit” in one connected sub graph, you could only choose the one in which the sum of weight of these edges is minimum).

  For example, we may get two possible sums:




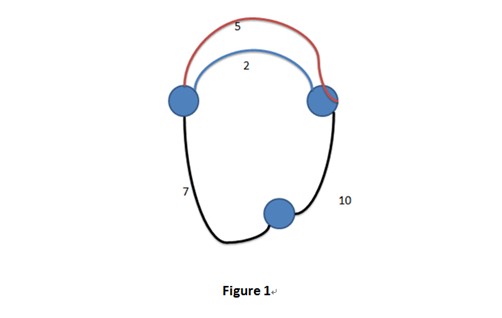
(1)  7 + 10 + 5 = 22

(2)  7 + 10 + 2 = 19

(There are two “Hamiltonian circuit” in this graph!)

 

Input

In the first line there is an integer T, indicates the number of test cases. (T <= 20)

In each case, the first line contains two integers n and m, indicates the number of vertices and the number of edges. (1 <= n <=1000, 0 <= m <= 10000)

Then m lines, each line contains three integers a,b,c ,indicates that there is one edge between a and b, and the weight of it is c . (1 <= a,b <= n, a is not equal to b in any way, 1 <= c <= 10000)

 

Output

Output “Case %d: “first where d is the case number counted from one. Then output “NO” if there is no way to get some connected sub graphs that any of them exists the Hamiltonian circuit after the delete operation. Otherwise, output
the minimum sum of weight you may get if you delete the edges in the optimal strategy.

 

Sample Input

3

3 4
1 2 5
2 1 2
2 3 10
3 1 7 

3 2
1 2 3
1 2 4

2 2
1 2 3
1 2 4

 

Sample Output

Case 1: 19
Case 2: NO
Case 3: 6

Hint

In Case 1:
You could delete edge between 1 and 2 whose weight is 5. 

In Case 2:
It’s impossible to get some connected sub graphs that any of them exists the Hamiltonian circuit after the delete operation.

 

Author

AekdyCoin

 

Source

2010 ACM-ICPC Multi-University Training Contest（1）——Host
by FZU

#include<stdio.h>
#include<string.h>
#include<queue>
using namespace std;
const int MAXN = 10010;
const int MAXM = 100100;
const int INF = 1<<30;
struct EDG{
    int to,next,cap,flow;
    int cost;  //每条边的单位价格
}edg[MAXM];
int head[MAXN],eid;
int pre[MAXN], cost[MAXN]  ; //点0~(n-1)

void init(){
    eid=0;
    memset(head,-1,sizeof(head));
}
void addEdg(int u,int v,int cap,int cst){
    edg[eid].to=v; edg[eid].next=head[u]; edg[eid].cost = cst;
    edg[eid].cap=cap; edg[eid].flow=0; head[u]=eid++;

    edg[eid].to=u; edg[eid].next=head[v]; edg[eid].cost = -cst;
    edg[eid].cap=0; edg[eid].flow=0; head[v]=eid++;
}

bool inq[MAXN];
bool spfa(int sNode,int eNode,int n){
    queue<int>q;
    for(int i=0; i<n; i++){
        inq[i]=false; cost[i]= INF;
    }
    cost[sNode]=0; inq[sNode]=1; pre[sNode]=-1;
    q.push(sNode);
    while(!q.empty()){
        int u=q.front(); q.pop();
        inq[u]=0;
        for(int i=head[u]; i!=-1; i=edg[i].next){
            int v=edg[i].to;
            if(edg[i].cap-edg[i].flow>0 && cost[v]>cost[u]+edg[i].cost){ //在满足可增流的情况下。最小花费
                cost[v] = cost[u]+edg[i].cost;
                pre[v]=i;   //记录路径上的边
                if(!inq[v])
                    q.push(v),inq[v]=1;
            }
        }
    }
    return cost[eNode]!=INF;    //推断有没有增广路
}
//反回的是最大流，最小花费为minCost
int minCost_maxFlow(int sNode,int eNode ,int& minCost,int n){
    int ans=0;
    while(spfa(sNode,eNode,n)){
        ans++;
        for(int i=pre[eNode]; i!=-1; i=pre[edg[i^1].to]){
            edg[i].flow+=1; edg[i^1].flow-=1;
            minCost+=edg[i].cost;
        }
    }
    return ans;
}
void scanf(int &ans){
    char ch;
    while(ch=getchar()){
        if(ch>='0'&&ch<='9')
            break;
    }
    ans=ch-'0';
    while(ch=getchar()){
        if(ch<'0'||ch>'9')
            break;
        ans=ans*10+ch-'0';
    }
}
int  mapt[1005][1005];
int main(){
    int T,_case=0,n,m , u, v, d ;
    scanf(T);
    while(T--){
        scanf(n); scanf(m);
        init();
        int s=0, t=2*n+1;

        for(int i=1; i<=n; i++){
            addEdg(s , i , 1 , 0);
            addEdg(i+n , t , 1 , 0);
            for(int j=1; j<=n; j++)
                mapt[i][j]=INF;
        }
        while(m--){
            scanf(u); scanf(v); scanf(d);
            if(mapt[u][v]>d)
                mapt[u][v]=mapt[v][u]=d;
        }
        for( u=1; u<=n; u++)
            for(v=1; v<=n; v++)
            if(mapt[u][v]!=INF)
                addEdg(u,v+n,1,mapt[u][v]);

        int mincost=0;
       n-= minCost_maxFlow(s , t , mincost , t+1);
       printf("Case %d: ",++_case);
        if(n==0)
            printf("%d\n",mincost);
        else
            printf("NO\n");
    }
}