EM and GMM（Code）

In EM and GMM（Theory）, I have introduced the theory of em algorithm for gmm. Now lets practice it in matlab!

1. Generate 1000 pieces of  random 2-dimention data which obey 5 gaussian distribution.

function X = GenerateData
    Sigma = [1, 0; 0, 1];
    mu1 = [1, -1];
    x1 = mvnrnd(mu1, Sigma, 200);
    mu2 = [5.5, -4.5];
    x2 = mvnrnd(mu2, Sigma, 200);
    mu3 = [1, 4];
    x3 = mvnrnd(mu3, Sigma, 200);
    mu4 = [6, 4.5];
    x4 = mvnrnd(mu4, Sigma, 200);
    mu5 = [9, 0.0];
    x5 = mvnrnd(mu5, Sigma, 200);
    % obtain the 1000 data points to be clustered
    X = [x1; x2; x3; x4; x5];
end

2. Complete em algorithm.

function [Mu, Sigma, Pi, r_nk] = EmForGmm(Data, classNum, initVal)
    % Data : Matrix(n * d), n is the quantity of the data and d is the data
    %        dimention
    % classNum : Scale
    % initVal : Cell(3 * 1), initial value for Mu, Sigma and Pi
    %           cell 1: Mu
    %           cell 2: Sigma
    %           cell 3: Pi
    [sampleNum, sampleDim] = size(Data);
    indexPoint = zeros(sampleNum, 1);
    while(1)
        for n = 1 : sampleNum
            x = Data(n, :);
            px_nk_sumk = 0;
            for k = 1 : classNum
                Sigma_k = initVal{2}(:,:,k);
                Mu_k = initVal{1}(k,:);
                Pi_k = initVal{3}(k);
                px(n,k) = (1/(2*pi^(sampleDim/2)*det(Sigma_k)^(0.5))) ...
                    * exp(-0.5 * (x - Mu_k)*inv(Sigma_k)*(x - Mu_k)');
                px_nk_sumk = px_nk_sumk + Pi_k * px(n, k);
            end
            for k = 1 : classNum
                Sigma_k = initVal{2}(:,:,k);
                Mu_k = initVal{1}(k,:);
                Pi_k = initVal{3}(k);
                r(n, k) = Pi_k * px(n, k) / px_nk_sumk;
            end
        end
        Nk = sum(r)';
        newMuK = r' * Data;
        Nkk = repmat(Nk,1,2);
        newMuK = newMuK ./ Nkk;
        for i = 1 : classNum
            nk = Nk(i);
            MuT = repmat(newMuK(i,:),sampleNum,1);
            xT = Data - MuT;
            rT = r(:,i);
            rT = repmat(rT,1,2);
            newSigma(:,:,i) = xT' * (xT .* rT) / nk;
        end
        newPiK = Nk / sampleNum;
        indexPointT = indexPoint;
        [aa,indexPoint] = max(r,[],2);
        j1 = sum(sum(abs(newMuK - initVal{1}))) < 1e-6;
        j2 = sum(sum(sum(abs(newSigma - initVal{2})))) < 1e-6;
        j3 = sum(abs(newPiK - initVal{3})) < 1e-6;
        clf;
        if (j1 && j2 && j3)
            for i = 1:sampleNum
                if (indexPoint(i)==1)
                    plot(Data(i,1), Data(i,2), 'r.')
                end
                if (indexPoint(i)==2)
                    plot(Data(i,1), Data(i,2), 'b.')
                end
                if (indexPoint(i)==3)
                    plot(Data(i,1), Data(i,2), 'k.')
                end
                if (indexPoint(i)==4)
                    plot(Data(i,1), Data(i,2), 'g.')
                end
                if (indexPoint(i)==5)
                    plot(Data(i,1), Data(i,2), 'm.')
                end
                hold on;
            end
            break;
        else
            initVal{1} = newMuK;
            initVal{2} = newSigma;
            initVal{3} = newPiK;
        end
    end
    Mu = newMuK;
    Sigma = newSigma;
    Pi = newPiK;
    r_nk = r;
end

　3. Complete main function.

clear,clc,clf
Data = GenerateData;
classNum = 5;
[sampleNum, sampleDia] = size(Data);

%% Initial value
% indexNum = floor(1 + (sampleNum - 1) * rand(1,classNum));
indexNum = [50,300,500,700,900];
initMu = Data(indexNum,:);

initSigmaT = [1 0.2;0.2 1];
initSigma = zeros(2,2,classNum);
for i = 1 : classNum
    initSigma(:,:,i) = initSigmaT;
    initPi(i,1) = 1 / classNum;
end
initVal = cell(3,1);
initVal{1} = initMu;
initVal{2} = initSigma;
initVal{3} = initPi;

%% EM algorithm
[Mu, Sigma, Pi, r_nk] = EmForGmm(Data, classNum, initVal);

4. Result.

The cluster result can be show as figure 3.

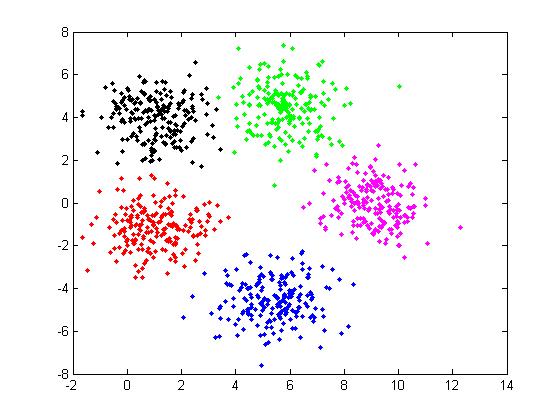
Figure 3

  The probality distribution function can be writen as:

\[  p(\mathbf{x}) = \sum_{k=1}^{K}\pi_kp(\mathbf{x}|\mu_k\Sigma_k)  \]

where,

  $\mu_1  =  (1.028, -1.158) $, $\mu_2  =  (5.423, -4.538) $, $\mu_3  =  (1.036, 3.975) $,  $\mu_4  =  (5.835, 4.474) $,  $\mu_5  =  (9.074, -0.063) $

Notice that, when generate the data:

$\mu_1  =  (1, -1) $, $\mu_2  =  (5.5, -4.5) $, $\mu_3  =  (1, 4) $, $\mu_4  =  (6, 4.5) $, $\mu_5  =  (9, 0) $)

---

\[
\Sigma_1 = \left(
\begin{array}{cc}
1.0873& 0.0376\\
0.0376& 0.8850
\end{array}
\right),
\Sigma_2 = \left(
\begin{array}{cc}
1.1426& 0.0509\\
0.0509& 0.9192
\end{array}
\right),
\Sigma_3 = \left(
\begin{array}{cc}
0.9752& -0.0712\\
-0.0712& 0.9871
\end{array}
\right),
\Sigma_4 = \left(
\begin{array}{cc}
1.0111& -0.0782\\
-0.0782& 1.2034
\end{array}
\right),
\Sigma_5 = \left(
\begin{array}{cc}
0.8665& -0.1527\\
-0.1527& 0.9352
\end{array}
\right)
\]

Notice that, when generate the data:

\[\Sigma = \left(
\begin{array}{cc}
1& 0\\
0& 1
\end{array}
\right)
\]

---

$\pi_1  =  0.1986$, $\pi_2  =  0.2004 $, $\pi_3  =  0.1992$,  $\pi_4  =  0.2015 $,  $\pi_5  =  0.2002$

Notice that, when generate the data:  each guassian components occupy 20% of all data. (1000 data point, 200 for each guassian components)