Slam笔记I

视觉Slam笔记I

第二讲-三位空间刚体运动

点与坐标系：

基础概念：

• 坐标系：左手系和右手系。右手系更常用。定义坐标系时，会定义世界坐标系，相机坐标系，以及其他关心对象的坐标系。空间中任意一点可由空间的基的线性表出。

• 加减法：用坐标描述更方便。

• 内积：点乘得数，即

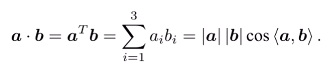
• 外积：叉乘得向量，即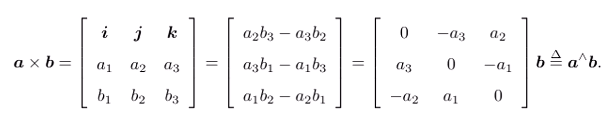右手系下，得到按照右手定则获取的向量。

• 坐标系间的变换：
  
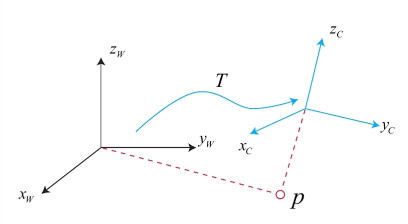
  通过平移(向量的加减)和旋转(有多种描述方式，见下)

• 2D情况：二维坐标点表示位置+一个旋转角表示朝向。

• 3D情况：三维坐标点表示位置+一个旋转角(角度间的变换使用旋转，旋转方式有多种，见下)。

旋转矩阵：（描述旋转的第一种方式）

坐标系 (e_1,e_2,e_3)经过旋转变成 (e'_1,e'_2,e'_3)，在三维空间中，向量 a保持不动，那么如何表出它在 (e'_1,e'_2,e'_3)下的坐标：

1. 线性表出法向量 a坐标：两坐标系实质是分别用两组不同的基去表示同一个点，则两者的线性组合是相等的：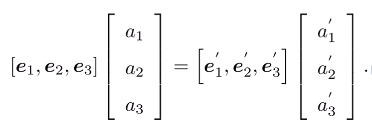
2. 左右两边同时左乘 (e_1,e_2,e_3)的转置，得到：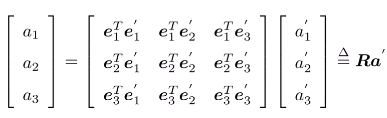

• R即为旋转矩阵。
• 性质：
  • R是一个正交矩阵（矩阵的逆即矩阵的转置，或转置×本身即为一个单位矩阵）。
  • R的行列式值为1。
• 满足上述性质的矩阵都可以称为旋转矩阵，使用集合表示： ，又称特殊正交群SO(3)。
• 固定表示方式（下标顺序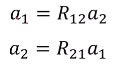）：且满足矩阵关系：。

因此，空间中不同坐标系下点坐标的变换可以使用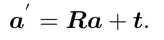：即旋转+平移的形式完全描述

• 理论依据：欧拉定理，刚体在三维空间中的一般运动，可分解为刚体上方某一点的平移，以及绕经过此点的旋转轴的转动。

但是，这种表示方式在多次进行变换时会有不便（），因此使用增广的方式进行表示：

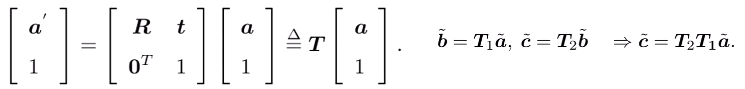
• 其中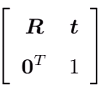，称为变换矩阵，的形式称为齐次坐标。
• 齐次坐标性质：齐次坐标乘上任意非0常数时仍表达同一坐标
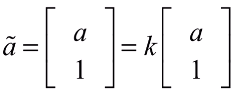
• 变换矩阵的集合：称为特殊欧式群SE(3)：

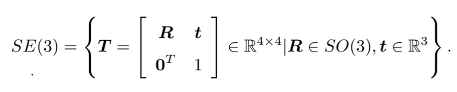
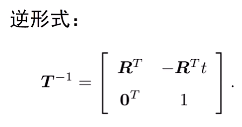
旋转向量和欧拉角：

旋转矩阵在实际中更常用，但这些概念也是需要清楚的。

旋转矩阵R是一个3×3的矩阵，有九个元素，但仅有三个自由度，也就是存在描述方式上的冗余，那么能否以更少的元素表达旋转？

刚体旋转存在一个转轴(向量)，还有转过的角度，于是想用角度乘以向量(单位化过后)的形式去描述旋转。

旋转向量

• 一个向量，方向为旋转轴方向，长度为转过的角度。(单位向量乘角度大小)

• 又称角轴/轴角。

• 罗德里格斯公式可以将旋转向量(n,theta)转换成旋转矩阵R：

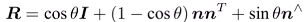
• 旋转矩阵R也可以转换成旋转向量(n,theta)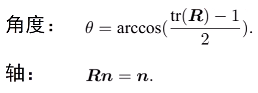：n是特征向量。

欧拉角

• 将旋转分解成三个方向上的转动，常用顺序为yaw-pitch-roll(也就是绕Z-Y-X方式转，注意 ，不同地方在绕Z转之后，所绕的Y轴可能是原来的Y轴，也可能是转动后的Y轴)
• 
• 万向锁(Gimbal Lock)：欧拉角存在奇异性(特定值下，旋转的自由度减1)
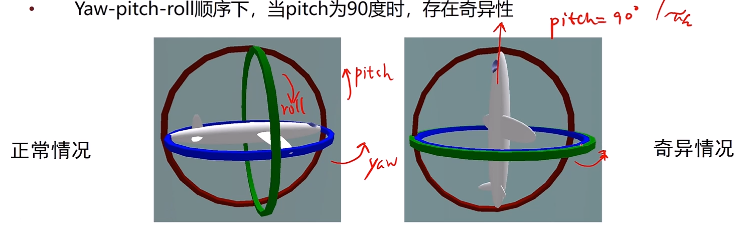• 在pitch方向旋转完毕后，roll方向旋转和yaw方向旋转是重合的。由此，欧拉角不适合插值或迭代，故不常用。

四元数：

吸取了旋转矩阵和旋转向量、欧拉角的优点，是一种优秀的描述方式。

• 2D情况下，可以用单位复数表达旋转：

\[z=x+iy=\rho e^{i\theta}
\]

• 用z乘以i，相当于旋转了90度(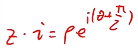)，乘-i转动-90度。

在三维情况下，四元数可作为扩充定义的复数

• 特点1：有三个虚部+一个实部

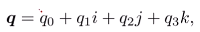
• 特点2：虚部之间存在关系：

• 单位四元数可以表达三维空间的旋转：

  

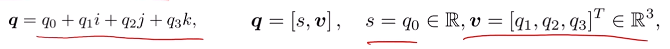
• 四元数也能定义很多运算：

  

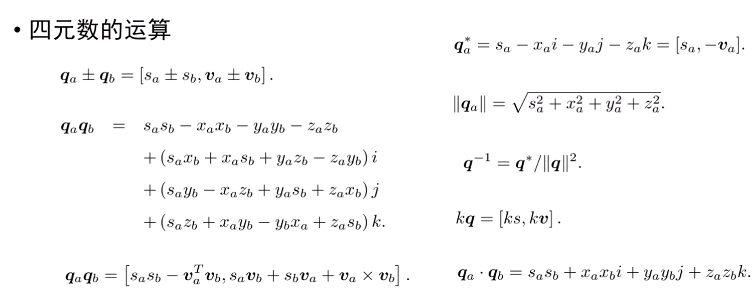
• 四元数转换成旋转向量：

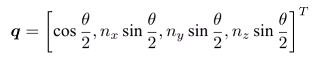
• 旋转向量转换成四元数：

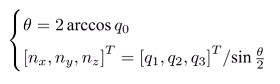
• 用四元数表示旋转：