wqs 二分

初看这个东西可能很难理解，我个人也学习了很多遍，然后发现这个直接理解实际上并不难。

wqs 二分主要是解决 恰好分成/选 \(k\) 段 这一类 DP 问题的算法。如果不知道形式可以看一下 P4983 忘情 这道题的题面。

在满足一个条件：

在 DP 其他给定条件不变的情况下，随着分段的段数的增加，最终 DP 出来的值先减小后增大或者先增大后减小，也就是最终的 DP 值在横坐标为分段的段数意义下形成一个上凸壳或者下凸壳（当然，一般而言都是先增大后减小）。

的情况下，我们可以在时间复杂度上用 \(\log\) 的时间换取不需要枚举分多少段。当分的段数与序列长度同阶时，这种算法可以大大优化复杂度。

其在 DP 意义下的本质是对于分出来的每一段加上一个权值 \(val\)。一般而言，我们分段问题的式子都可以写成如下形式：

\[f_i={\min/\max}_j(f_j+w_{j,i})
\]

而我们将其改成

\[f_i={\min/\max}_j(f_j+w_{j,i})-val
\]

的形式。

这样有什么好处呢？可以显而易见的发现，这个时候，分段变成了一个有一定代价的事情。

原来我们必须枚举分多少段这一维是因为分段本身是没有代价的，而当分段有了代价之后，我们就可以通过控制 \(val\) 的值来改变分的段数。

（注意，这里的 \(val\) 是可正可负的）

然后，我们就可以在几何意义上大致去感受一下这个的过程是什么。

先盗一张图。（%蛙）

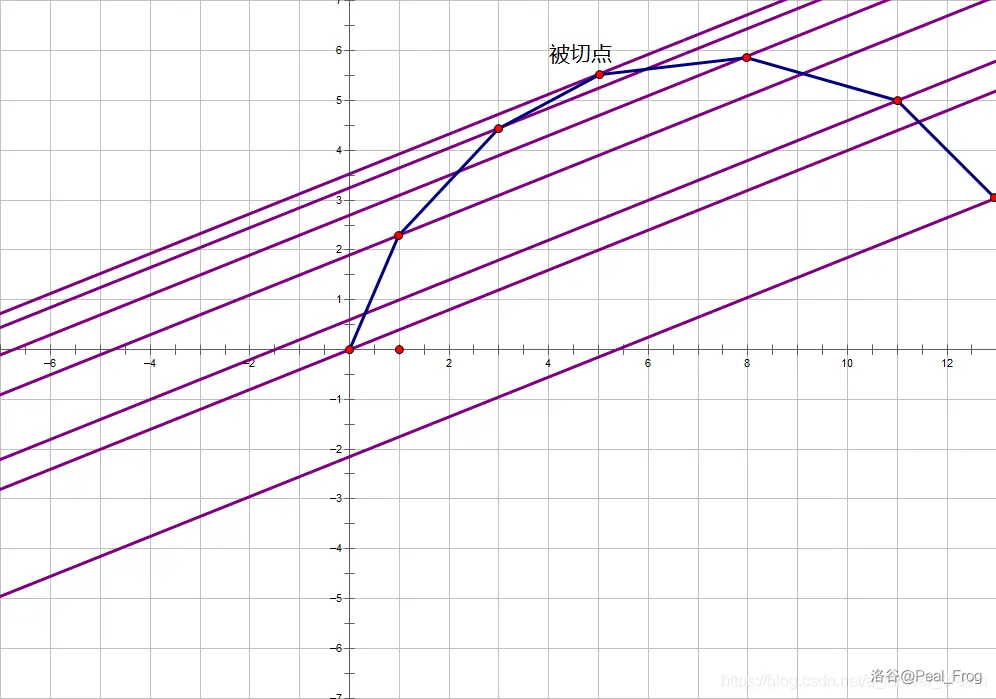
这里的 \(x\) 轴指代的是分多少段，\(y\) 轴指代的是 DP 最终 的答案。这样，这个蓝色的上凸壳指代的就是对于分每一个对应的段，最终 DP 出来的值是多少。

假设我们要求的是那个所谓被切点的值，也就是我们要求要分 \(5\) 段，去求其 DP 值。

这里有很多紫色线，我们假设其为 \(y=kx+b\)。这里每个红色的点都有一条斜率相同的紫色线穿过。

可以发现，对于每一条紫色线，\(b\) 对应的值相比于原来的值，对应减少了 \(x\) 个 \(k\)。这有什么用呢？由于我们 DP 的时候，每分一段就会减去一个 \(val\)，因此 这里的 \(b\) 值表示 \(val=k\) 的时候 DP 出来的值。

同时，由于这是一个上凸壳，因此我们可以去二分紫色线的斜率。当紫色线切到的点的横坐标就是我们要求的将序列分出来的段数，我们就可以通过 \(y=kx+b\) 来求出答案。

因此，wqs 二分的主体代码就比较明晰了。设要求分 \(m\) 段。

int l=-1e18,r=1e18,ans=0;
while(l<=r){
	int mid=(l+r)>>1;check(mid);
	if(g[n]<=m) r=mid-1,ans=mid;
	else l=mid+1;
}
check(ans);ans=f[n]+m*ans;

这里的 check 函数指代的就是原始的 DP，当然，DP 时需要减去二分的 \(mid\)。

而 \(f_n\) 表示 DP 出来的最终答案，\(g_n\) 表示 DP 出来最终答案是分为多少段的。

注意，由于可能出现原始的凸壳上多个点共线的情况，因此我们在答案相同时统一使分出来的段数尽量小，使得二分出来的 \(ans\) 可以取到。

当然，个人由于代码习惯，更喜欢在 DP 的时候 \(+val\)，最后统计答案的时候 \(-m*ans\)。可以发现这是等效的。

注意，wqs 二分由于有凸性，因此很喜欢和斜率优化结合在一起。因此在做 wqs 二分的题前请先学习 斜率优化。

P4983 忘情

显然化简一下就可以发现式子与平均数一分钱关系没有。有转移

\[f_i=\min_{j<i}(f_j+(s_i-s_j+1)^2)
\]

其中 \(s\) 表示前缀和。这个东西一眼斜率优化。然后通过 wqs 二分将分的段数去掉即可。

可以发现分的段数越多一定优，因此这个函数是严格递减的。因此如果要切到壳上的点斜率一定是负的。但由于我上面提到过的我的写法，因此二分的 \(val\) 一定是正的。可以通过这个略卡一丁点常数。

code

为什么要卡常数呢？因为我只会不动脑子的李超线段树优化 DP，完全不会单调队列来维护，因此复杂度是 \(n\log n\log C\) 的，其中 \(C\) 是二分的范围。然后就比单调队列的 \(n\log C\) 慢了很多倍，然后就要卡常，比如调 \(C\) 的范围。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=4e5+7,inf=1e18+7;
int n,m,a[N],s[N],f[N],g[N],tr[N],tmp[N],loc[N],len,sign[N],tot;
struct node{int b,k;}seg[N];
#define ls (u<<1)
#define rs (u<<1|1)
int get(int id,int x){return seg[id].b+seg[id].k*x;}
bool cmp(int u,int v,int x){return get(u,x)<get(v,x);}
void update(int u,int l,int r,int x){
	if(sign[u]!=tot) tr[u]=0,sign[u]=tot;
	int mid=(l+r)>>1;
	if(cmp(x,tr[u],s[mid])) swap(x,tr[u]);if(l==r) return;
	if(cmp(x,tr[u],s[l])) update(ls,l,mid,x);
	if(cmp(x,tr[u],s[r])) update(rs,mid+1,r,x);
}
int query(int u,int l,int r,int x){
	if(sign[u]!=tot) tr[u]=0,sign[u]=tot;
	if(l==r) return tr[u];
	int mid=(l+r)>>1,res=x<=mid?query(ls,l,mid,x):query(rs,mid+1,r,x);
	return cmp(tr[u],res,s[x])?tr[u]:res;
}
void check(int val){
	seg[0]={inf,0};
	for(int i=1;i<=n;i++){
		int j=query(1,1,n,i),tmp1=(s[i]+1)*(s[i]+1)+val,tmp2=get(j,s[i])+s[i]*s[i]+val;
		if(tmp1<=tmp2) f[i]=tmp1,g[i]=1;else f[i]=tmp2,g[i]=g[j]+1;
		seg[i]={f[i]+(s[i]-1)*(s[i]-1),-2*(s[i]-1)};
		update(1,1,n,i);
	}
}
signed main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i],s[i]=s[i-1]+a[i];
	int l=0,r=1e15,ans=0;
	while(l<=r){
		int mid=(l+r)>>1;check(mid);tot++;
		if(g[n]<=m) r=mid-1,ans=mid;
		else l=mid+1;
	}
	check(ans);
	cout<<f[n]-ans*m<<'\n';
	return 0;
}

P6246 [IOI 2000] 邮局 加强版 加强版

不知道为什么是黑，感觉和上一道题差不多。（要不把上一道题升黑？）

显然有（将取 \(\min\) 省掉）

\[f_i=f_j+w_{i,j}
\]

可能这道题最困难的就是看出如何 \(O(1)\) 得到 \(w_{i,j}\)。机房大佬给出了一个很牛的式子

\[w_{j,i}=s_i+s_j-s_{\left \lfloor \frac{i+j}{2} \right \rfloor }-s_{\left \lceil \frac{i+j}{2} \right \rceil }
\]

可以发现这个东西就是对的。

然后我们仍然使用传统的李超线段树来做。发现这个东西显然就不是一次函数了，初看感觉不好维护。

但是谁说李超线段树只能维护线段了？实际上只要是能 \(O(1)\) 求函数值，严格单增/严格单减的函数就可以做。显然对于一个固定的 \(j\)，\(i\) 越大 \(w_{j,i}\) 单增。

然后就可以利用类似的逻辑去维护了，还可以省去离散化之类的东西。

code

但是注意，由于我们统一要求在权值相同的情况下分的段数少，因此在函数比较的时候要求在函数值相等的时候谁对应分出来的段少更优。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e6+7,inf=1e18+7;
int n,m,a[N],pre[N],suf[N],sign[N],tot,tr[N],g[N],f[N];
#define ls (u<<1)
#define rs (u<<1|1)
int get(int l,int r){return f[l]+pre[r]+pre[l]-pre[(l+r)>>1]-pre[(l+r+1)>>1];}
bool cmp(int u,int v,int x){int tmp1=get(u,x),tmp2=get(v,x);return tmp1==tmp2?g[u]<g[v]:tmp1<tmp2;}
void update(int u,int l,int r,int x){
	if(sign[u]!=tot)tr[u]=0,sign[u]=tot;
	int mid=(l+r)>>1;
	if(cmp(x,tr[u],mid)) swap(x,tr[u]);
	if(cmp(x,tr[u],l)) update(ls,l,mid,x);
	if(cmp(x,tr[u],r)) update(rs,mid+1,r,x);
}
int query(int u,int l,int r,int x){
	if(sign[u]!=tot)tr[u]=0,sign[u]=tot;
	if(l==r) return tr[u];
	int mid=(l+r)>>1,res=x<=mid?query(ls,l,mid,x):query(rs,mid+1,r,x);
	return cmp(tr[u],res,x)?tr[u]:res;
}
void check(int val){
	for(int i=1;i<=n;i++){
		int j=query(1,1,n,i);
		f[i]=get(j,i)+val,g[i]=g[j]+1;
		update(1,1,n,i);
	}
}
signed main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];sort(a+1,a+n+1);for(int i=1;i<=n;i++) pre[i]=pre[i-1]+a[i];
	int l=0,r=1e9,ans=0;
	while(l<=r){
		int mid=(l+r)>>1;check(mid);tot++;
		if(g[n]<=m) ans=mid,r=mid-1;
		else l=mid+1;
	}
	check(ans);cout<<f[n]-ans*m;
	return 0;
}

P4383 [八省联考 2018] 林克卡特树

这道题主要的难点个人认为应该是基础的树形 DP。

首先我们要转化题意，原问题等价于选原来树中不交的恰好 \(k+1\) 条链，使得这这些链的权值最大。

一个比较直观的想法是设 \(f_{u,i}\) 表示 \(u\) 及其子树中选 \(i\) 条链的方案数。但是发现这样没办法转移，因为没有办法统计是否已经有了边连。

然后发现由于我们是选链上的点，因此 切之后 点的度数只可能是 \(0,1,2\)。其中度数为 \(0\) 代表不选。但是这样没有办法将单独一个点这种情况划分出来，因此我们让单独一个点的情况归结到度数为二的情况中，也就是不能再连边，其本身已经为一个独立连通块。

具体而言，我们设 \(f_{u,i,0/1/2}\) 表示 \(u\) 及其子树内切出来了 \(i\) 条链，切之后 \(u\) 的度数为 \(0/1/2\) 的最大权值。初始化对于每个 \(u\)，有 \(f_{u,0,0}=0,f_{u,1,2}=0\)，其他所有东西全部赋为 \(-\infty\)。

然后转移就是对于 \(u\) 的每一个儿子 \(v\)，有：

1. 不选 \(u,v\) 之间的边，那这就是两个独立的连通块，\(u\) 的度数不会改变。但是我们还是要加上 \(v\) 的贡献，直接枚举切出来的链的数量对应相加。
2. 选 \(u,v\) 之间的边。那就要分讨了。首先 \(u\) 的度数一定会加一，因此原本度数是二的不能够转移，然后大概讨论一下，比如 \(u,v\) 原来度数都是一的时候是 将两条原本独立的链合并，变成一条链，因此链数会减一。之类的转移上的细节可以看完后在代码里详细看一下。

最终的答案就是 \(f_{1,k+1,0/1/2}\) 中的最大值。然后我们就有了 \(O(nk)\) 的 DP，考虑如何优化一下。

发现一个事实，就是在其他条件不变的情况下，以 \(k+1\) 为 \(x\) 轴，最终的答案会形成一个上凸壳。

感性理解一下，就是当不砍边或者砍的边较少的时候，答案与原本树的直径比较接近。当砍的数量比较适中的时候，我们可以将所有的负边全部砍掉，将所有正边连成一条直线，这个时候答案有最大值。然后砍边的数量继续增加的时候，由于要求了恰好砍 \(k\) 条边，因此只能将一些正边也砍了，这样答案就会下降，一直到将所有边全部砍完变成 \(0\)。

然后直接 wqs 二分做完了，把枚举 \(i\) 条链的那一维去掉，直接做。复杂度 \(O(n\log C)\)。

code

注意这道题是取最大值，同时因为我自己的写法，导致了二分的时候应该在 DP 出来砍的段数小于等于 \(k+1\) 的时候让 \(l=mid+1\) 而不是取最小值的时候令 \(r=mid-1\)。就因为这个调了一个半小时也是没谁了。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=3e5+7,inf=1e16+7;
struct node{int v,w;};
struct edge{int w,g;}f[N][3],tmp[3];
edge operator + (const edge &x,const edge &y){return {x.w+y.w,x.g+y.g};}
bool operator < (const edge &x,const edge &y){return x.w==y.w?x.g>y.g:x.w<y.w;}
vector <node> q[N];
int n,k,tot[N];
void dfs(int u,int fa,int val){
	for(int i=0;i<tot[u];i++){
		int v=q[u][i].v,w=q[u][i].w;if(v==fa) continue;
		dfs(v,u,val);for(int j=0;j<=2;j++) {tmp[j]={-inf,inf};for(int k=0;k<=2;k++)tmp[j]=max(tmp[j],f[u][j]+f[v][k]);}//根本就不连边
		tmp[1]=max({tmp[1],f[u][0]+f[v][1]+(edge){w,0},f[u][0]+f[v][0]+(edge){w+val,1}});
		tmp[2]=max({tmp[2],f[u][1]+f[v][0]+(edge){w,0},f[u][1]+f[v][1]+(edge){w-val,-1}});
		for(int j=0;j<=2;j++)f[u][j]=tmp[j];
	}
}
void init(int val){for(int i=1;i<=n;i++) f[i][0]={0,0},f[i][1]={-inf,inf},f[i][2]={val,1};}
signed main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>k;for(int i=1,u,v,w;i<=n-1;i++){cin>>u>>v>>w,q[u].push_back({v,w}),tot[u]++,q[v].push_back({u,w}),tot[v]++;}
	int l=-1e12,r=1e12,ans=0;
	while(l<=r){
		int mid=(l+r)>>1;init(mid);dfs(1,0,mid);edge tmp1=max({f[1][0],f[1][1],f[1][2]});
		if(tmp1.g<=k+1){ans=mid,l=mid+1;}else r=mid-1;
	}
	init(ans);dfs(1,0,ans);cout<<max({f[1][0],f[1][1],f[1][2]}).w-(k+1)*ans;
	return 0;
}