Java数据结构（十三）—— 二叉排序树（BST）

二叉排序树（BST)

需求

给定数列{7，3，10，12，5，1，9}，要求能够高效的完成对数据的查询和添加

思路三则

1. 使用数组，缺点：插入和排序速度较慢

2. 链式存储，添加较快，但查找速度慢

3. 使用二叉排序树

基本介绍

对于二叉排序树的任何一个非叶子节点，要求左子节点的值比当前节点的值小，右子节点的值比当前节点的值大

图解

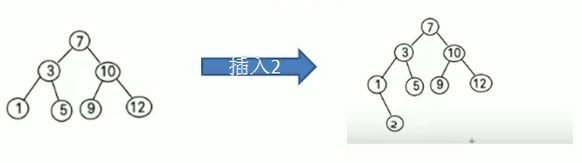
步骤

1. 从数列取出第一个数成为根节点

2. 取出第二个数，从根结点开始比较，大于当前节点，与右子节点比较，小于当前节点与左子节点比较

3. 直到放到叶子节点

4. 取出剩余的数值，重复上述步骤

建立二叉排序树

代码实现：BinarySortTree.java

package com.why.binary_sort_tree;
​
/**
 * @Description TODO 建立二叉排序树
 * @Author why
 * @Date 2020/12/1 14:38
 * Version 1.0
 **/
public class BinarySortTreeDemo {
    public static void main(String[] args) {
        int[] arr = {7,3,10,12,5,1,9};
        BinarySortTree bst = new BinarySortTree();
        for (int i = 0; i < arr.length; i++) {
            Node node = new Node(arr[i]);
            bst.add(node);
        }
        System.out.println("中序遍历二叉排序树；");
        bst.midOrder();
    }
}
​
/**
 * 二叉排序树
 */
class BinarySortTree{
    private Node root;
​
    /**
     * 添加节点
     * @param node
     */
    public void add(Node node){
        if (root == null){//直接放上
            root = node;
        }else {
            root.add(node);
        }
    }
​
    /**
     * 中序遍历
     */
    public void midOrder(){
        if (root != null){
            root.midOrder();
        }else {
            System.out.println("二叉排序树为空");
        }
    }
}
/**
 * 节点类
 */
class Node{
    int value;
    Node left;
    Node right;
​
    public Node(int value) {
        this.value = value;
    }
​
    /**
     * 添加节点，递归形式，需满足二叉排序树的要求
     * @param node
     */
    public void add(Node node){
        if (node == null){
            return;
        }
        //判断传入的节点的值和当前子树的根节点的值的关系
        if (node.value < this.value){
            if (this.left == null){//当前节点左子节点为空
                this.left = node;
            }else {//不为空，递归向左子树添加
                this.left.add(node);
            }
        }else {
            if (this.right == null){
                this.right = node;
            }else {
                this.right.add(node);
            }
        }
    }
​
    /**
     * 中序遍历
     */
    public void midOrder(){
        if (left != null){
            this.left.midOrder();
        }
        System.out.println(this);
        if (this.right != null){
            this.right.midOrder();
        }
    }
​
    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }
}

二叉排序树删除

删除的节点是叶子节点

思路

1. 先找到要删除的节点targetNode

2. 找到targetNode的父节点parent

3. 确定targetNode是parent的左子节点还是右子节点

4. 根据前面的情况对应删除

删除的节点只有一棵子树的情况

思路

1. 先找到要删除的节点targetNode

2. 找到targetNode的父节点parent

3. 确定targetNode的子节点是左子节点还是右子节点

4. 确定targetNode是parent的左子节点还是右子节点

5. 如果targetNode有左子节点

   • targetNode是parent的左子节点 parent.left = targetNode.left

   • targetNode是parent的右子节点parent.right = tsrgetNode.left

6. 如果targetNode有右子节点

   • targetNode是parent的左子节点parent.left = targetNode.right

   • targetNode是parent的右子节点parent.right = psrent.right

删除的节点有两颗子树

思路

1. 先找到要删除的节点targetNode

2. 找到targetNode的父节点parent

3. 从targetNode的右子树找到最小的节点

4. 用一个临时变量，将最小的节点的值保存temp

5. 删除最小节点

6. targetNode.value = temp.value

代码实现

package com.why.binary_sort_tree;
​
/**
 * @Description TODO 建立二叉排序树
 * @Author why
 * @Date 2020/12/1 14:38
 * Version 1.0
 **/
public class BinarySortTreeDemo {
    public static void main(String[] args) {
        int[] arr = {7,3,10,12,5,1,9,0,2,4,6,8,};
        BinarySortTree bst = new BinarySortTree();
        for (int i = 0; i < arr.length; i++) {
            Node node = new Node(arr[i]);
            bst.add(node);
        }
        System.out.println("中序遍历二叉排序树；");
        bst.midOrder();
​
        System.out.println("删除后");
        bst.deleteNode(5);
        bst.midOrder();
​
    }
}
​
/**
 * 二叉排序树
 */
class BinarySortTree{
    private Node root;
​
    /**
     * 添加节点
     * @param node
     */
    public void add(Node node){
        if (root == null){//直接放上
            root = node;
        }else {
            root.add(node);
        }
    }
​
    /**
     * 中序遍历
     */
    public void midOrder(){
        if (root != null){
            root.midOrder();
        }else {
            System.out.println("二叉排序树为空");
        }
    }
​
    /**
     * 查找需删除的节点
     * @param value
     * @return
     */
    public Node search(int value){
        if (root == null){
            return null;
        }else {
            return root.search(value);
        }
    }
​
    /**
     * 查找父节点
     * @param value
     * @return
     */
    public Node searchParent(int value){
        if (root == null){
            return null;
        }else {
            return root.searchParent(value);
        }
    }
​
    public void deleteNode(int value){
        if (root == null){
            return;
        }else {
            //找到需删除的节点
            Node targetNode = search(value);
            if (targetNode == null){//未找到
                return;
            }
            //如果二叉排序树只有一个节点
            if (root.left == null && root.right == null){
                return;
            }
​
            //查找需删除的节点的父节点
            Node parent = searchParent(value);
            if (targetNode.left == null && targetNode.right == null){//删除的节点是叶子节点
                //判断targetNode是父节点的左子节点还是右子节点
                if (parent.left != null && parent.left.value == value){//是左子节点
                    parent.left = null;
                }else if (parent.right != null && parent.right.value == value){//是右子节点
                    parent.right = null;
                }
            }else if ((targetNode.left != null && targetNode.right == null) ||
                    (targetNode.right != null && targetNode.left == null)) {//只有一棵子树
                    //确定targetNode的节点是左节点还是右节点
                    if (targetNode.left != null) {//左子节点
                        if (parent != null){//非根节点
                            //确定targetNode是parent的左子节点还是右子节点
                            if (parent.left.value == value) {//左子节点
                                parent.left = targetNode.left;
                            } else {//右子节点
                                parent.right = targetNode.left;
                            }
                        }else {
                            root = targetNode.left;
                        }
                    } else {//右子节点
                        if (parent != null){
                            //确定targetNode是parent的左子节点还是右子节点
                            if (parent.left.value == value) {//左子节点
                                parent.left = targetNode.right;
                            } else {//右子节点
                                parent.right = targetNode.right;
                            }
                        }else {
                            root = targetNode.right;
                        }
                    }
            }else {//删除的节点有两颗子树
                //找到最小值并删除
                int minValue = deleteRightMin(targetNode.right);
                //将最小值赋值给targetNode.value
                targetNode.value = minValue;
            }
        }
    }
​
    /**
     * 寻找最小值
     * @param node
     * @return
     */
    public int deleteRightMin(Node node){
        Node target = node;
        while (target.left != null){
            target = target.left;
        }
        //这时target指向最小节点
        //删除最小节点
        deleteNode(target.value);
        //返回最小节点的value
        return target.value;
    }
}
/**
* 节点类
*/
class Node{
    int value;
    Node left;
    Node right;
​
    public Node(int value) {
        this.value = value;
    }
​
    /**
     * 添加节点，递归形式，需满足二叉排序树的要求
     * @param node
     */
    public void add(Node node){
        if (node == null){
            return;
        }
        //判断传入的节点的值和当前子树的根节点的值的关系
        if (node.value < this.value){
            if (this.left == null){//当前节点左子节点为空
                this.left = node;
            }else {//不为空，递归向左子树添加
                this.left.add(node);
            }
        }else {
            if (this.right == null){
                this.right = node;
            }else {
                this.right.add(node);
            }
        }
    }
​
    /**
     * 中序遍历
     */
    public void midOrder(){
        if (left != null){
            this.left.midOrder();
        }
        System.out.println(this);
        if (this.right != null){
            this.right.midOrder();
        }
    }
​
    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }
​
    /**
     * 寻找需要删除的节点
     * @param value
     * @return
     */
    public Node search(int value){
        if (value == this.value){//找到
            return this;
        }else if (value < this.value){//向左子树查找
            if (this.left == null){
                return null;
            }
            return this.left.search(value);
        }else {//向右子树查找
            if (this.right == null){
                return null;
            }
            return this.right.search(value);
        }
    }
​
    /**
     * 查找需要删除节点的父节点
     * @param value
     * @return
     */
    public Node searchParent(int value){
        if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)){
            //找到父节点返回当前节点
            return this;
        }else {
            //如果查找的值小于当前节点的值
            if (value < this.value && this.left != null){//左子树查找
                return this.left.searchParent(value);
            }else if (value >= this.value && this.right != null){//右子树查找
                return this.right.searchParent(value);
            }else {
                return null;//没有找到父节点
            }
        }
    }
}
​