PTA天梯赛校内模拟

最长对称子串 || 区间dp || 马拉车

dp[i][j]表示区间[i, j]是否为回文串，若是则为1，不是则为0。

边界条件：

1. 区间长度为1，dp为1。(奇数个字符递推的起始情况)

2. 区间长度为2，且两个字符相同，则dp为1。(偶数个字符递推的起始情况)

3. 右边界不超过n。

转移：

当区间长度大于2时，若dp[l+1][r-1] == 1 && s[l] == s[r]，那么dp[l][r] = 1；

第一维遍历区间长度，第二维遍历左端点。通过这两维可以确定区间右端点的位置，若满足条件则转移。由于转移是从小区间到大区间，而最外层循环是从小区间开始，所以递推成立。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

bool dp[1111][1111];
char s[1111];
int main()
{
    scanf("%[^\n]", s + 1);//读入一行，gets可能有的oj不支持
    int n = strlen(s + 1), r;
    int ans = 1;
    for(int i = 1; i <= n; ++i) {
        for (int l = 1; l <= n; ++l) {
            r = l + i - 1;
            if (r > n) break;
            if (i == 1) dp[l][l] = 1;
            else if (i == 2 && s[l] == s[r])
            {
                dp[l][r] = 1;
                ans = max(ans, 2);
            }
            else if (i > 2 && s[l] == s[r] && dp[l + 1][r - 1] == 1)
            {
                dp[l][r] = 1;
                ans = max(ans, i);
            }
        }
    }
    cout << ans << endl;
    return 0;
}

列车调度 || 模拟&set使用

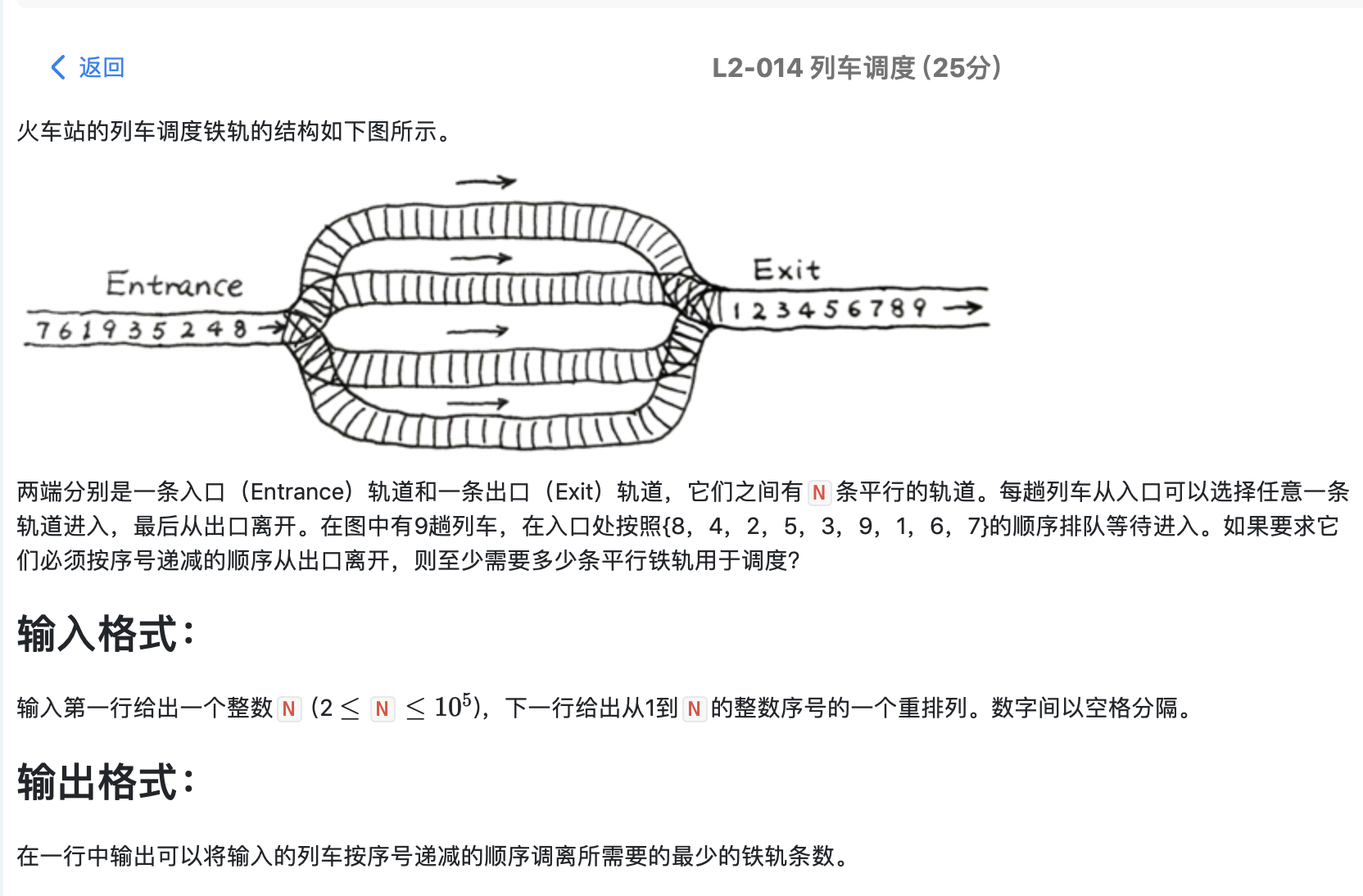
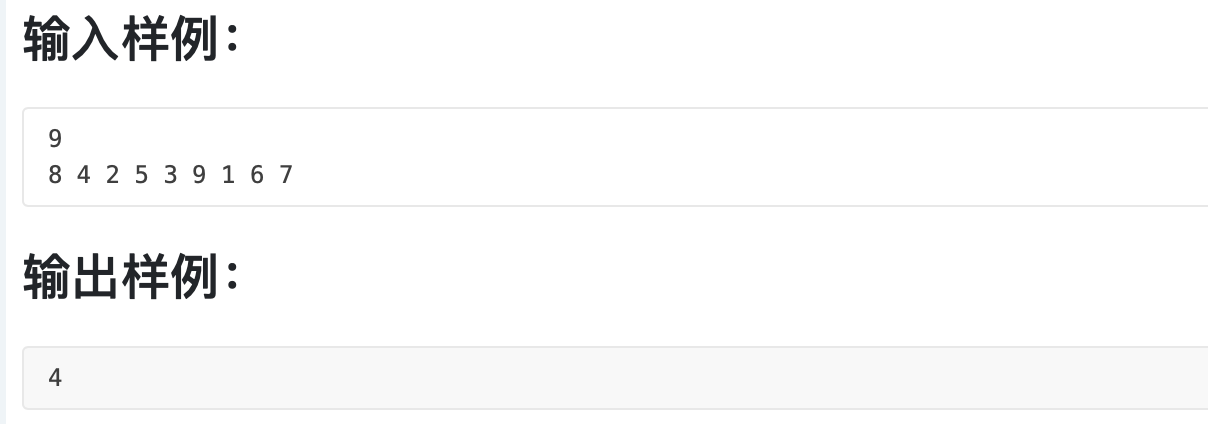
遍历，单调递减的一个连续序列一定属于一个队列，若不是，则将该元素与各个队列最小的元素进行比较，找到大于它的最小的那个元素。

我们用set维护各个队列最小的元素集合，而set的大小则为当前需要队列的个数。

#include <bits/stdc++.h>
using namespace std;

set<int> s;
int n;

int main()
{
    scanf("%d", &n);
    int mx = 0, x;
    for(int i = 0; i < n; i++)
    {
        scanf("%d", &x);
        auto it = s.lower_bound(x);
        if(it == s.end())  s.insert(x);
        else
        {
            s.erase(it);
            s.insert(x);
        }
        mx = max(mx, (int)s.size());
    }
    printf("%d\n", mx);
}

红色警报 || dfs&连通块

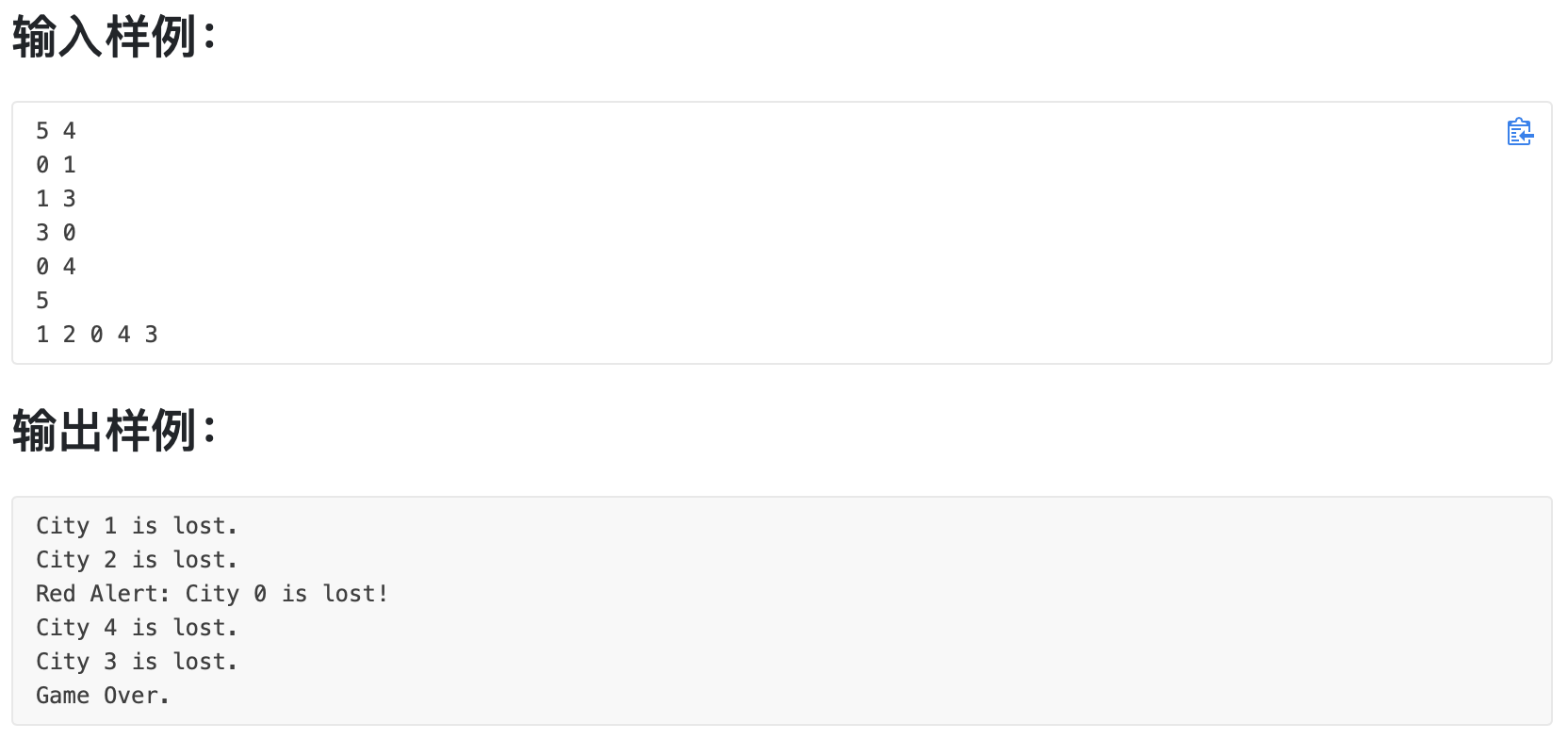
如何判断失去一个城市，国家的连通性发生变化？当然是连通块的个数发生变化。

那么考虑连通块的数目将如何变化呢？可能不变，可能变多(注意，可能不止多1)，可能变少(由于有一个连通块为单独的一个点，删除这个点后连通块数目-1)。

数据范围很小，那就暴力呀！每次删除一个城市，计算连通块数目，若变多，则说明国家的连通性发生了变化，反之不变。

vis数组表示每次dfs时是否已经访问过该节点，mark数组用于标记已经失去的城市，它们已经无法访问。

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;

vector<int> G[555];
bool vis[555];
bool mark[555];

int cnt;

void dfs(int s)
{
    vis[s] = 1;//放在这里，而不是下面那个if下面，否则可能从s来，又回到了s
    for(int i = 0; i < G[s].size(); ++i)
    {
        if(!vis[G[s][i]] && !mark[G[s][i]])
        {
            dfs(G[s][i]);
        }
    }
}

int main()
{
    int n, m, x, y, r, s;
    cin >> n >> m;
    for(int i = 1; i <= m; ++i)
    {
        scanf("%d %d", &x, &y);
        if(x == y) continue;
        G[x].push_back(y);
        G[y].push_back(x);
    }
    cin >> r;
    for(int j = 0; j < n; ++j)
    {
        if(!vis[j])
        {
            dfs(j);
            ++cnt;
        }
    }
    int pr = cnt;
    for(int i = 1; i <= r; ++i)
    {
        cnt = 0;
        fill(vis, vis + n, 0);
        scanf("%d", &s);
        mark[s] = 1;
        for(int j = 0; j < n; ++j)
        {
            if(!vis[j] && !mark[j])
            {
                dfs(j);
                ++cnt;
            }
        }
        if(cnt >= pr + 1)//不一定只多1呀！
            cout << "Red Alert: City " << s << " is lost!" << endl;
        else cout << "City " << s << " is lost." << endl;
        if(i == n) cout << "Game Over." << endl;
        pr = cnt;
    }
}

p.s. 连通块个数不仅可以dfs，还可以用并查集实现。

这里dfs的方法是最外层大循环一次dfs每个点，若已经访问过，就不dfs，若没有，则dfs，并且连通块数cnt++；