2019 南京网络赛 B super_log 【递归欧拉降幂】

一、题目

　　super_log

二、分析

　　公式很好推出来，就是$$a^{a^{a^{a^{...}}}}$$一共是$b$个$a$。

　　对于上式，由于指数太大，需要降幂，这里需要用到扩展欧拉定理：

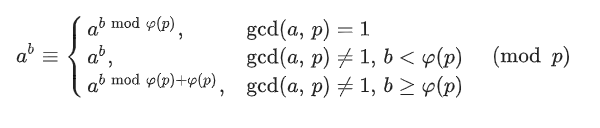
　　用这个定理时，除了$\gcd (a,p) =1$的情况，其他情况主要是保证$a$的指数不为$0$,在写代码的时候也需要注意这点，当然也可以重新定义个快速幂，使其快速幂的结果保证不为$0$，也是可以的的。

三、AC代码

#include <bits/stdc++.h>

using namespace std;
#define ll long long
#define Min(a,b) ((a)>(b)?(b):(a))
#define Max(a,b) ((a)>(b)?(a):(b))
#define P pair<int, int>

const int MAXN = 1e6+5;
int Phi[MAXN], Prime[MAXN], nPrime;

void Euler()
{
    memset(Phi, 0, sizeof(Phi));
    Phi[1] = 1;
    nPrime = 0;
    for(int i = 2; i < MAXN; i++)
    {
        if(!Phi[i]) //i为素数
        {
            Phi[i] = i - 1;
            Prime[nPrime++] = i;
        }
        for(int j = 0; j < nPrime && (long long)i*Prime[j] < MAXN; j++)
        {
            if(i%Prime[j])
            {

                Phi[ i*Prime[j] ] = Phi[i]*(Prime[j]-1);
            }
            else
            {
                Phi[ i*Prime[j] ] = Phi[i]*Prime[j];
                break;
            }
        }
    }
    return;
}

ll gcd(ll a, ll b) {return b==0?a:gcd(b,a%b);}

ll Pow(ll a, ll b, ll mod)
{
    ll ans = 1;
    while(b) {
        if(b&1) ans = ans*a%mod;
        a = a * a % mod;
        b>>=1;
    }
    return ans;
}

ll qPow(ll a, ll b, ll mod)
{
    ll ans = 1;
    while(b) {
        if(b&1) ans = (ans * a > mod ? ans * a % mod + mod : ans * a);
        a = (a * a > mod ? a * a % mod + mod : a * a);
        b>>=1;
    }
    return ans;
}

ll solve(ll a, ll times, ll m)
{
    if(m == 1)  return 1;
    if(times == 0)  return 1;
    ll res = Phi[m];
    ll b = solve(a, times-1, res);
    if(gcd(a, m) == 1)
        return Pow(a, b%res, m);
    else if(b && b < res)
        return Pow(a, b, m);
    else
        return Pow(a, b%res + res, m);
}

ll solve2(ll a, ll times, ll m)
{
    if(times == 0)  return 1;
    if(m == 1)  return 1;
    return qPow(a, solve2(a, times-1, Phi[m]), m);
}

int main()
{
    freopen("input.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    int T;
    ll a, b, m;
    scanf("%d", &T);
    Euler();
    while(T--) {
        scanf("%lld%lld%lld", &a, &b, &m);
        printf("%lld\n", solve2(a, b, m)%m);
        // printf("%lld\n", solve(a, b, m)%m);
    }
    return 0;
}