4.15 省选模拟赛 编码 trie树 前缀和优化建图 2-sat

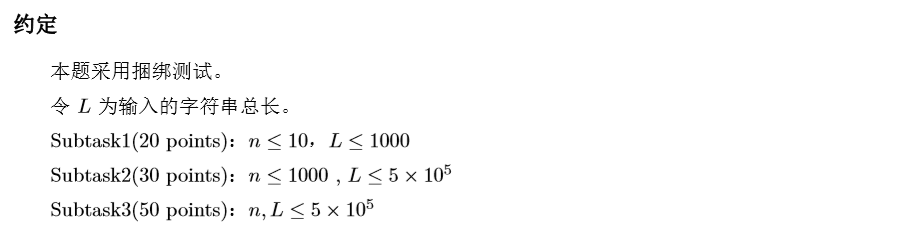
好题 np.

对于20分 显然可以爆搜。

对于50分 可以发现每个字符串上的问号要么是0,要么是1.考虑枚举一个字符串当前是0还是1 这会和其他字符串产生矛盾。

所以容易 发现这是一个2-sat问题。

拆点 把任意两个产生矛盾的字符串进行连边。然后最后判矛盾即可。

n^2枚举 建图 判断矛盾时使用字符串hash 要分类讨论4种情况。

using namespace std;
const int MAXN=1010,maxn=500010,cc1=19260817,cc2=114514;
int n,mark,cnt,top,id,len;
string a[MAXN];
int flag[MAXN],c[MAXN<<1],low[MAXN<<1],dfn[MAXN<<1],s[MAXN<<1];
int lin[MAXN<<1],ver[MAXN*MAXN<<2],nex[MAXN*MAXN<<2],w[MAXN];
vector<int>h0[MAXN];//表示为0时的前缀hash值 或者表示什么都不是的前缀hash值.
vector<int>h1[MAXN];//表示为1时的前缀hash值
struct wy
{
	int len,id;
}t[MAXN];
inline int cmp(wy a,wy b){return a.len<b.len;}
inline void dfs(int x)
{
	low[x]=dfn[x]=++cnt;
	s[++top]=x;
	go(x)
	{
		if(!dfn[tn])
		{
			dfs(tn);
			low[x]=min(low[x],low[tn]);
		}
		else if(!c[tn])low[x]=min(low[x],dfn[tn]);
	}
	if(dfn[x]==low[x])
	{
		int y=0;++id;
		while(y!=x)
		{
			y=s[top--];
			c[y]=id;
		}
	}
}
inline void add(int x,int y)
{
	ver[++len]=y;
	nex[len]=lin[x];
	lin[x]=len;
}
int main()
{
	freopen("code.in","r",stdin);
	freopen("code.out","w",stdout);
	ios::sync_with_stdio(false);
	cin>>n;
	if(n<=1000)
	{
		rep(1,n,i)
		{
			cin>>a[i];
			t[i]=(wy){a[i].size(),i};
		}
		rep(1,n,i)
		{
			ll w0=0,w1=0;
			rep(0,((int)a[i].size())-1,j)
			{
				w0=w0*P%mod;
				w1=w1*P%mod;
				if(a[i][j]=='?')
				{
					flag[i]=j+1;
					w0=(w0+cc1)%mod;
					w1=(w1+cc2)%mod;
				}
				else
				{
					if(a[i][j]=='0')w1=(w1+cc1)%mod,w0=(w0+cc1)%mod;
					else w1=(w1+cc2)%mod,w0=(w0+cc2)%mod;
				}
				h0[i].pb(w0);
				h1[i].pb(w1);
			}
		}
		//x表示这个点选择0 x+n表示这个点选择1.
		sort(t+1,t+1+n,cmp);
		rep(1,n,i)
		{
			int x=t[i].id;//x.len<=y.len
			int xx=t[i].len;
			rep(i+1,n,j)
			{
				int y=t[j].id;
				if(!flag[x]&&(!flag[y]||flag[y]>xx))
				{
					if(h0[x][xx-1]==h0[y][xx-1])
					{
						puts("NO");
						return 0;
					}
					continue;
				}
				if(!flag[x]&&flag[y]<=xx)
				{
					if(h0[x][xx-1]==h0[y][xx-1])add(y,y+n);
					if(h0[x][xx-1]==h1[y][xx-1])add(y+n,y);
					continue;
				}
				if(flag[x]&&(!flag[y]||flag[y]>xx))
				{
					if(h0[x][xx-1]==h0[y][xx-1])add(x,x+n);
					if(h1[x][xx-1]==h0[y][xx-1])add(x+n,x);
				}
				if(flag[x]&&flag[y]<=xx)
				{
					if(h0[x][xx-1]==h0[y][xx-1])add(x,y+n),add(y,x+n);
					if(h0[x][xx-1]==h1[y][xx-1])add(x,y),add(y+n,x+n);
					if(h1[x][xx-1]==h0[y][xx-1])add(x+n,y+n),add(y,x);
					if(h1[x][xx-1]==h1[y][xx-1])add(x+n,y),add(y+n,x);
				}
			}
		}
		rep(1,n+n,i)if(!dfn[i])dfs(i);
		rep(1,n,i)if(c[i]==c[i+n]){puts("NO");return 0;}
		puts("YES");
	}
	return 0;
}

考虑100分。

我考试的时候想了一波trie树 但是当时思考没有在这个暴力的基础上思考 所以 建图也很麻烦 所以弃疗了。

可以发现我们拆过点后 把这些串给放到trie树上。

可以发现连边的时候 使用前缀和连边 即可优化建图了。

对于某个节点存放多个节点 这个时候 对这个节点内部再进行一次前缀和优化建图。

对于某个节点不存在? 考虑子树内和链上上的节点都需要自己向自己的对立连边 这个使用懒标记即可。

上传标记和 标记的时候注意判断不合法的情况。

这个优化建图还是很精髓的。充分的利用了trie树的性质。

注意空间不要开小了 计算不了点数可以开到空间上界小一点。

const int MAXN=500010*3;
int n,sum,cnt=1,top,id,len,last=1,mark;
string a[MAXN];
int t[MAXN][2],ne[MAXN],pos[MAXN];
int flag[MAXN],c[MAXN<<3],low[MAXN<<3],dfn[MAXN<<3],s[MAXN<<3],w1[MAXN],w2[MAXN];
int lin[MAXN<<3],ver[MAXN<<3],nex[MAXN<<3],add1[MAXN],add2[MAXN];
vector<int>g[MAXN];
inline void dfs(int x)
{
	low[x]=dfn[x]=++cnt;
	s[++top]=x;
	go(x)
	{
		if(!dfn[tn])
		{
			dfs(tn);
			low[x]=min(low[x],low[tn]);
		}
		else if(!c[tn])low[x]=min(low[x],dfn[tn]);
	}
	if(dfn[x]==low[x])
	{
		int y=0;++id;
		while(y!=x)
		{
			y=s[top--];
			c[y]=id;
		}
	}
}
inline void add(int x,int y)
{
	ver[++len]=y;
	nex[len]=lin[x];
	lin[x]=len;
}
inline void insert(int x,int op)
{
	int p=1,c=min(x,ne[x]);
	for(ui i=0;i<a[c].size();++i)
	{
		int w=a[c][i]-'0';
		if(!t[p][w])t[p][w]=++cnt;
		p=t[p][w];
	}
	if(op)g[p].pb(x);
	else
	{
		if(add1[p])mark=1;
		add1[p]=1,add2[p]=1;
	}
	pos[x]=p;
}
inline void dfs(int x,int fa)
{
	int s1=++sum,s2=++sum;
	if(w1[fa])add(s1,w1[fa]);//w1[x]表示当前点向前缀所有的点的相反点的连边
	if(w2[fa])add(w2[fa],s2);//w2[x]表示前缀所有的点向当前点的连边.
	int c1=++sum,c2=++sum,cc1,cc2;//c1表示当前这个点对前缀和的相反点的连边.
	//c2表示前缀和的所有点对当前点的连边.
	for(ui i=0;i<g[x].size();++i)
	{
		int tn=g[x][i];
		//cout<<tn<<endl;
		add(tn,c1);
		cc1=++sum;
		add(cc1,c1);
		add(cc1,ne[tn]);
		c1=cc1;
		add(c2,ne[tn]);
		cc2=++sum;
		add(c2,cc2);
		add(tn,cc2);
		c2=cc2;
		if(w1[fa])add(tn,w1[fa]);
		if(w2[fa])add(w2[fa],ne[tn]);
		add(s1,ne[tn]);
		add(tn,s2);
	}
	//puts("ww");
	w1[x]=s1;w2[x]=s2;
	if(t[x][0])add1[t[x][0]]|=add1[x],dfs(t[x][0],x);//传递子树标记
	if(t[x][1])add1[t[x][1]]|=add1[x],dfs(t[x][1],x);
	if(add2[x]&&add2[t[x][0]])mark=1;
	if(add2[x]&&add2[t[x][1]])mark=1;
	add2[x]|=add2[t[x][0]];//传递链上标记.
	add2[x]|=add2[t[x][1]];
}
int main()
{
	freopen("code.in","r",stdin);
	freopen("code.out","w",stdout);
	ios::sync_with_stdio(false);
	cin>>n;//cout<<1<<endl;
	rep(1,n,i)cin>>a[i];
	rep(1,n,i)
	{
		ne[i]=i+n;ne[i+n]=i;
		for(ui j=0;j<a[i].size();++j)if(a[i][j]=='?'){flag[i]=j+1;break;}
		if(flag[i])
		{
			a[i][flag[i]-1]='0';
			insert(i,1);
			a[i][flag[i]-1]='1';
			insert(i+n,1);
		}
		else insert(i,0);
	}
	sum=2*n;dfs(1,0);
	if(mark){puts("NO");return 0;}
	rep(1,2*n,i)if(add1[pos[i]]||add2[pos[i]])if(pos[i])add(i,ne[i]);
	rep(1,2*n,i)if(!dfn[i])dfs(i);
	rep(1,n,i)if(c[i]==c[i+n]){puts("NO");return 0;}
	puts("YES");
	return 0;
}