Gym - 101982F 扫描线+线段树

题目链接：https://codeforces.com/gym/101982/attachments

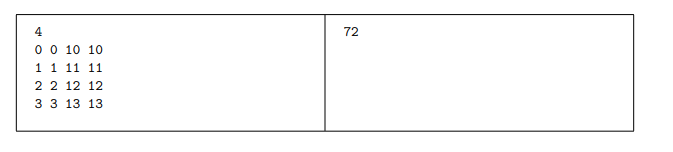
要你求覆盖奇数次的矩形面积并，每次更新时减去原先的值即可实现奇数次有效，下推时为保证线段长度不变左儿子的值为x[mid]-x[l]再减原来的值，右儿子的值为x[r]-x[mid]再减原来的值

#include<iostream>
#include<algorithm>
using namespace std;
#define ll long long
#define maxn 200005
struct seg{
    ll l,r,h,s;
    seg(){}
    seg(ll l,ll r,ll h,ll s):l(l),r(r),h(h),s(s){};
    bool operator <(const seg &a)const{
        return h<a.h;
    }
}se[maxn];
ll sum[maxn<<],lazy[maxn<<],x[maxn];
void pushup(ll rt)
{
    sum[rt]=sum[rt<<]+sum[rt<<|];
}
void pushdown(ll rt,ll l,ll r)
{
    if(lazy[rt])
    {
        lazy[rt<<]^=;
        lazy[rt<<|]^=;
        ll mid=l+r>>;
        sum[rt<<]=x[mid]-x[l]-sum[rt<<];
        sum[rt<<|]=x[r]-x[mid]-sum[rt<<|];
        lazy[rt]=;
    }
}
void update(ll L,ll R,ll l,ll r,ll rt)
{
    if(L<=l&&R>=r)
    {
        lazy[rt]^=;
        sum[rt]=x[r]-x[l]-sum[rt];
        return ;
    }
    ll mid=l+r>>;
    pushdown(rt,l,r);
    if(L<mid)update(L,R,l,mid,rt<<);
    //因为往右更新时是mid到r 不是mid+1到r 所以L<=mid 会造成死循环 如l=l r=2 L=2 R=3 mid=1
    if(R>mid)update(L,R,mid,r,rt<<|);
    pushup(rt);
}
int main()
{
    int n,x1,x2,y1,y2,tot=;
    cin>>n;
    for(int i=;i<=n;i++)
    {
        cin>>x1>>y1>>x2>>y2;
        x[tot]=x1;
        se[tot++]=seg(x1,x2,y1,);
        x[tot]=x2;
        se[tot++]=seg(x1,x2,y2,-);
    }
    x[]=-;
    sort(x+,x+tot);
    sort(se+,se+tot);
    int nx=unique(x,x+tot)-x;
    ll ans=;
    for(int i=;i<tot-;i++)
    {
        ll l=lower_bound(x,x+nx,se[i].l)-x;
        ll r=lower_bound(x,x+nx,se[i].r)-x;
        update(l,r,,nx,);
        ans+=sum[]*(se[i+].h-se[i].h);
    }
    cout<<ans<<endl;
    return ;
}