——————————————先讲原理，如下：——————————————————

举一个详细的例子：

一般场景，要访问的域名：www.jizhuomi.com/android，文件名为down.zip

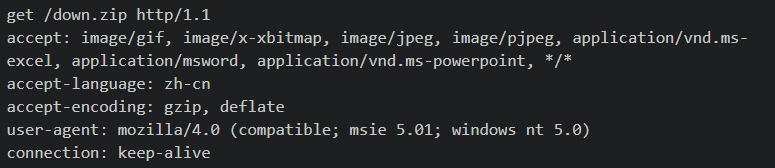
服务器到请求后，按要求寻找请求的文件，提取文件的信息，然后返回给浏览器，返回信息如下

好了。现在讲解一下断点续传原理：

所谓断点续传，也就是要从文件已经下载的地方开始继续下载。因此，在客户端，浏览器传给web服务器的时候要多加一条信息--从哪里开始。

比方说，“浏览器”来传递请求信息给服务器，要求从2000070字节开始：

range: bytes=2000070-  这个就是浏览器对服务器喊话：“喂！服务器，down.zip这个文件从2000070字节开始传过来！前面的字节不用传了哈~”

服务器说：“好嘞！您等着~”，返回如下（返回的代码也改为206了，而不再是200了）：

——————————————原理到此结束——————————————————

http断点续传的原理的更多相关文章

  1. .net断点续传的原理

    在了解HTTP断点续传的原理之前,先来说说HTTP协议,HTTP协议是一种基于tcp的简单协议,分为请求和回复两种.请求协议是由客户机(浏览器)向服务器(WEB SERVER)提交请求时发送报文的协议 ...

  2. 客户端HTTP断点续传的原理

    其实断点续传的原理很简单,就是在Http的请求上和一般的下载有所不同而已. 打个比方,浏览器请求服务器上的一个文时,所发出的请求如下:假设服务器域名为wwww.scu.edu.cn,文件名为down. ...

  3. PHP 实现断点续传的原理和方法

    PHP 实现断点续传的原理和方法 0. http协议从1.1开始支持静态获取文件的部分内容,为多线程下载和断点续传提供了技术支持.它通过在Header里两个参数实现的,客户端发请求时对应的是Accep ...

  4. HTTP文件断点续传的原理

    前几天一个同事跑过来找我说,我们在广告素材视频这块想做断点续传,就是这次某个视频缓存到一半,下次不用重头开始,可以在原来停留得位置开始继续下载.以提供更好的用户体验. 同时说需要我们支持吐素材地址的业 ...

  5. Java--使用多线程下载,断点续传技术原理(RandomAccessFile)

    一.基础知识 1.什么是线程?什么是进程?它们之间的关系? 可以参考之前的一篇文章:java核心知识点学习----并发和并行的区别,进程和线程的区别,如何创建线程和线程的四种状态,什么是线程计时器 简 ...

  6. QT断点续传（原理:需要在HTTP请求的header中添加Rang节,告诉服务器从文件的那个位置开始传输.格式为bytes 开始传输的位置）

    //功能:    根据一个URL地址将数据保存到指定路径下,支持断点续传//参数:    url            --需要访问的URL地址//         SavePath       -- ...

  7. 很简单的Java断点续传实现原理

    原理解析 在开发当中,"断点续传"这种功能很实用和常见,听上去也是比较有"逼格"的感觉.所以通常我们都有兴趣去研究研究这种功能是如何实现的? 以Java来说,网 ...

  8. C# 断点续传原理与实现

    在了解HTTP断点续传的原理之前,让我们先来了解一下HTTP协议,HTTP协议是一种基于tcp的简单协议,分为请求和回复两种.请求协议是由 客户机(浏览器)向服务器(WEB SERVER)提交请求时发 ...

  9. HTTP断点续传下载的原理

    frombegintoend原文HTTP断点续传下载的原理 要实现断点续传下载文件,首先要了解断点续传的原理.断点续传其实就是在上一次下载断开的位置开始继续下载,HTTP协议中,可以在请求报文头中加入 ...

随机推荐

  1. Lombok 详解

    简介 lombok是一个编译级别的插件,它可以在项目编译的时候生成一些代码.通俗的说,lombok可以通过注解来标示生成getter settter等代码. 引入 创建gradle项目 compile ...

  2. nginx模块之ngx_http_fastcgi_module

    nginx支持LNMP 安装php-fpm yum install php-fpm -y 使用/etc/php-fpm.d/www.conf配置文件默认配置即可 打开php配置: vim /etc/n ...

  3. css中content-box和border-box当宽度为百分比时的位置区别，vw和%区别

    盒模型 参考代码 // CSS 部分 <style> .box1,.box2{ width: 200px; height: 200px; padding: 20px; margin: 20 ...

  4. Win10安装3 —— U盘启动工具安装

    本文内容皆为作者原创,如需转载,请注明出处:https://www.cnblogs.com/xuexianqi/p/12364593.html 一:准备一个空U盘 U盘容量推荐至少8个G,先提前备份好 ...

  5. 小sun的假期【牛客】

    链接:https://ac.nowcoder.com/acm/contest/1085/A来源:牛客网 应肖老师要求前来更新水一水 题目描述 小 sun 非常喜欢放假,尤其是那种连在一起的长假,在放假 ...

  6. Wannafly Camp 2020 Day 6F 图与三角形 - 图论

    把黑边视为无边,那么答案之和每个点的度数有关 #include <bits/stdc++.h> using namespace std; #define int long long int ...

  7. nginx 无法启动：bind() to 0.0.0.0:443 failed

    bind to 0.0.0.0:443 failed.其实就是443端口被其它程序占用,要结束占用443端口导致nginx不能启动的应用. CMD: 1.查看所有程序使用的端口 netstat -ao ...

  8. 避免layui form表单重复触发submit绑定事件

    个人博客 地址:http://www.wenhaofan.com/article/20180927002336 在使用以下代码监听lay-filter为editConfig的提交按钮后,当点击提交按钮 ...

  9. 给IDEA添加右键打开功能

    添加文件夹右键程序打开 开始运行regedit 找到 HKEY_LOCAL_MACHINE\SOFTWARE\Classes\Directory\shell 1.右键shell目录新建项Idea 2. ...

  10. jdbc中SQL语句拼接java变量

    例如:String sql = "select * from user where username='" + username + "' and password =' ...