洛谷 2403 [SDOI2010] 所驼门王的宝藏

题目描述

在宽广的非洲荒漠中，生活着一群勤劳勇敢的羊驼家族。被族人恭称为“先知”的Alpaca L. Sotomon是这个家族的领袖，外人也称其为“所驼门王”。所驼门王毕生致力于维护家族的安定与和谐，他曾亲自率军粉碎河蟹帝国主义的野蛮侵略，为族人立下赫赫战功。所驼门王一生财宝无数，但因其生性节俭低调，他将财宝埋藏在自己设计的地下宫殿里，这也是今天Henry Curtis故事的起点。Henry是一个爱财如命的贪婪家伙，而又非常聪明，他费尽心机谋划了这次盗窃行动，破解重重机关后来到这座地下宫殿前。

整座宫殿呈矩阵状，由R×C间矩形宫室组成，其中有N间宫室里埋藏着宝藏，称作藏宝宫室。宫殿里外、相邻宫室间都由坚硬的实体墙阻隔，由一间宫室到达另一间只能通过所驼门王独创的移动方式——传送门。所驼门王为这N间藏宝宫室每间都架设了一扇传送门，没有宝藏的宫室不设传送门，所有的宫室传送门分为三种：

1. “横 天门”：由该门可以传送到同行的任一宫室；

2. “纵 寰门”：由该门可以传送到同列的任一宫室；

3. “自 由门”：由该门可以传送到以该门所在宫室为中心周围8格中任一宫室（如果目标宫室存在的话）。

深谋远虑的Henry当然事先就搞到了所驼门王当年的宫殿招标册，书册上详细记录了每扇传送门所属宫室及类型。而且，虽然宫殿内外相隔，但他自行准备了一种便携式传送门，可将自己传送到殿内任意一间宫室开始寻宝，并在任意一间宫室结束后传送出宫。整座宫殿只许进出一次，且便携门无法进行宫室之间的传送。不过好在宫室内传送门的使用没有次数限制，每间宫室也可以多次出入。

现在Henry已经打开了便携门，即将选择一间宫室进入。为得到尽多宝藏，他希望安排一条路线，使走过的不同藏宝宫室尽可能多。请你告诉Henry这条路线最多行经不同藏宝宫室的数目。

输入输出格式

输入格式：

输入文件sotomon.in第一行给出三个正整数N, R, C。

以下N行，每行给出一扇传送门的信息，包含三个正整数xi, yi, Ti，表示该传送门设在位于第xi行第yi列的藏宝宫室，类型为Ti。Ti是一个1~3间的整数，1表示可以传送到第xi行任意一列的“横天门”，2表示可以传送到任意一行第yi列的“纵寰门”，3表示可以传送到周围8格宫室的“自 由门”。

保证1≤xi≤R，1≤yi≤C，所有的传送门位置互不相同。

输出格式：

输出文件sotomon.out只有一个正整数，表示你确定的路线所经过不同藏宝宫室的最大数目。

输入输出样例

输入样例#1：

10 7 7
2 2 1
2 4 2
1 7 2
2 7 3
4 2 2
4 4 1
6 7 3
7 7 1
7 5 2
5 2 1

输出样例#1：

9

说明

数据规模和约定：

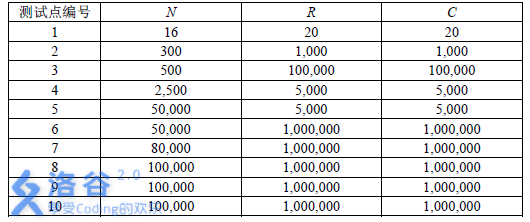
题解：

建图，缩点，然后跑最长路。T了很久，后来发现自己确实太暴力了。如果暴力建图，同一行或列之间连边可能会爆，同一行传送门类型都为1的点最后一定是一个连通分量，

所以可以直接连成一个环，再从这个环上任意一个点向同行的其它点连边，穿传送门类型为2的同理。跑最长路的时候，我跑了n遍spfa，然后学到了DAG上可以拓扑排序+DP

找起点终点不定的最长路，dp[i]表示以i结束的最长路的长度，按照拓扑序更新，这样用i去更新其它点时，可以保证i已经最优了，避免重复更新。

#include<bits/stdc++.h>
#define nn 2000010
#define mm 4000010
#define inf -100000000
using namespace std;
map<pair<int,int>,int> fi;
pair<int,int> in;
int xi[8]={-1,-1,-1,0,0,1,1,1},yi[8]={-1,0,1,-1,1,-1,0,1};
int x[nn],y[nn];
int fir[nn<<1],nxt[mm<<1],to[mm<<1],ti[nn],li[nn],rep[nn],sta[nn],mo[nn<<1],dis[nn<<1],q[nn<<1],du[nn<<1];
bool vis[nn<<1];
int e=0,l=0,t=0,ne,h;
int read()
{
    int ans=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {ans=ans*10+ch-'0';ch=getchar();}
    return ans*f;
}
void add(int u,int v)
{
    nxt[++e]=fir[u];fir[u]=e;to[e]=v;
}
int cmp1(int a,int b)
{
    if(x[a]==x[b])
      return ti[a]<ti[b];
    return x[a]<x[b];
}
int cmp2(int a,int b)
{
    if(y[a]==y[b])
      return ti[a]<ti[b];
    return y[a]<y[b];
}
void tarjan(int now)
{
    int sum=1;
    vis[now]=1;
    ti[now]=li[now]=++l;sta[++t]=now;
    for(int i=fir[now];i;i=nxt[i])
      if(!ti[to[i]])                  ////
      {
          tarjan(to[i]);
          li[now]=min(li[now],li[to[i]]);
      }
      else if(vis[to[i]]&&li[now]>ti[to[i]])                 ////
          li[now]=ti[to[i]];               ////
    if(li[now]==ti[now])
    {
        ne++;
        while(sta[t]!=now)
        {
            vis[sta[t]]=0;
            rep[sta[t]]=ne;
            sum++;
            t--;
        }
        mo[ne]=sum;
        rep[sta[t]]=ne;
        vis[sta[t]]=0;t--;
    }
}
int dp(int n)
{
    int o,an=-1;
    while(h<=t)
    {
        o=q[h++];
        if(dis[o]>an)
          an=dis[o];
        for(int i=fir[o];i;i=nxt[i])
        {
            du[to[i]]--;
            if(dis[to[i]]<dis[o]+mo[to[i]])
              dis[to[i]]=dis[o]+mo[to[i]];
            if(!du[to[i]])
              q[++t]=to[i];
        }
    }
    return an;
}
int main()
{
//    freopen("o.txt","r",stdin);
//    freopen("o.out","w",stdout);
    int n=read(),r=read(),c=read();
    ne=n;
    for(int i=1;i<=n;i++)
    {
        in.first=read();in.second=read();
        x[i]=in.first;y[i]=in.second;
        ti[i]=read();
        fi[in]=i;
        li[i]=i;
    }
    for(int i=1;i<=n;i++)
      if(ti[i]==3)
        for(int j=0;j<8;j++)
        {
            in.first=x[i]+xi[j];
            in.second=y[i]+yi[j];
            if(fi.find(in)!=fi.end())
              add(i,fi[in]);
        }
    sort(li+1,li+n+1,cmp1);
    for(int i=1;i<=n;i++)
      {
          int fi=0,la=0,j;
          for(j=i;j<=n&&x[li[i]]==x[li[j]];j++)
          if(ti[li[j]]==1)
          {
                if(!fi) fi=j;
                la=j;
                if(fi!=la)
                  add(li[j-1],li[j]);
        }
          if(fi)
          {
              if(fi!=la)
                add(li[la],li[fi]);
              for(j=i;j<=n&&x[li[i]]==x[li[j]];j++)
                if(ti[li[j]]!=1)
                  add(li[la],li[j]);
          }
          i=j-1;
      }
    for(int i=1;i<=n;i++)
      li[i]=i;
    sort(li+1,li+n+1,cmp2);
    for(int i=1;i<=n;i++)
      {
          int fi=0,la=0,j;
          for(j=i;j<=n&&y[li[i]]==y[li[j]];j++)
          if(ti[li[j]]==2)
          {
                if(!fi) fi=j;
                la=j;
                if(fi!=la)
                  add(li[j-1],li[j]);
        }
          if(fi)
          {
              if(fi!=la)
              add(li[la],li[fi]);
              for(j=i;j<=n&&y[li[i]]==y[li[j]];j++)
                if(ti[li[j]]!=2)
                  add(li[la],li[j]);
          }
          i=j-1;
      }
    fill(ti,ti+n+1,0);
    fill(li,li+n+1,0);
    for(int i=1;i<=n;i++)
      if(!ti[i])
        tarjan(i);
    for(int i=1;i<=n;i++)
      for(int j=fir[i];j;j=nxt[j])
        if(rep[i]!=rep[to[j]])
        {
            add(rep[i],rep[to[j]]);
            du[rep[to[j]]]++;
        }
    h=1,t=0;
    for(int i=n+1;i<=ne;i++)
      if(!du[i])
      {
          q[++t]=i;
          dis[i]=mo[i];
      }
    printf("%d",dp(n));
    return 0;
}