@NOIP2018 - D1T1@ 铺设道路

@题目描述@
@考场上的思路@
@比较正常的题解@

@题目描述@

春春是一名道路工程师，负责铺设一条长度为 n 的道路。

铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 n 块首尾相连的区域，一开始，第 i 块区域下陷的深度为 di。

春春每天可以选择一段连续区间 [L,R]，填充这段区间中的每块区域，让其下陷深度减少 1。在选择区间时，需要保证，区间内的每块区域在填充前下陷深度均不为 0。

春春希望你能帮他设计一种方案，可以在最短的时间内将整段道路的下陷深度都变为 0 。

输入

输入文件包含两行，第一行包含一个整数 n，表示道路的长度。第二行包含 n 个整数，相邻两数间用一个空格隔开，第 i 个整数为 di。

输出

输出文件仅包含一个整数，即最少需要多少天才能完成任务。

输入样例#1：

6

4 3 2 5 3 5

输出样例#1：

9

样例解释1：

一种可行的最佳方案是，依次选择： [1,6]、[1,6]、[1,2]、[1,1]、[4,6]、[4,4]、[4,4]、[6,6]、[6,6]。

数据规模与约定

对于 30% 的数据，1 ≤ n ≤ 10；

对于 70% 的数据，1 ≤ n ≤ 1000；

对于 100% 的数据，1 ≤ n ≤ 100000 , 0 ≤ di ≤ 10000。

@考场上的思路@

我抄我自己？

虽然这是 NOIP2013 的原题“积木游戏”……然而我并没有做过-_-

所以考场上想了一个比较复杂的解：

显然观察样例，我们可以贪心地这样做：对于某一个区间，选择最小值，将这个区间减去这个最小值，然后把区间按照这个最小值分为两个区间分治求解。

因此，本来想写线段树来着……但是我及时地发现（其实是因为不想写再多想会儿hhhh）区间的最小值是不会变化的。也就是说我们可以不去动态查询区间最小值，而是建成笛卡尔树，再在笛卡尔树上进行操作。

代码（不建议参考，建议继续往后看正常的解）：

#include<cstdio>

#include<stack>

using namespace std;

typedef long long ll;

const int MAXN = 100000;

const int MAXD = 10000;

struct node{

    ll ans; int d;

    node *ch[2];

}tree[MAXN + 5], *tcnt, *NIL, *root;

void init() {

    root = NIL = tcnt = &tree[0];

    NIL->ch[0] = NIL->ch[1] = NIL;

}

node *newnode(int d) {

    tcnt++;

    tcnt->d = d; tcnt->ch[0] = tcnt->ch[1] = NIL;

    return tcnt;

}

stack<node*>stk;

int d[MAXN + 5];

void dfs(node *rt, int x) {

    if( rt == NIL ) return ;

    dfs(rt->ch[0], rt->d);

    dfs(rt->ch[1], rt->d);

    rt->ans = rt->ch[0]->ans + rt->ch[1]->ans + (rt->d - x);

}

int main() {

    init(); int n;

    scanf("%d", &n);

    for(int i=1;i<=n;i++)

        scanf("%d", &d[i]);

    for(int i=1;i<=n;i++) {

        node *nw = newnode(d[i]), *lst = NIL;

        while( !stk.empty() && stk.top()->d > nw->d ) {

            lst = stk.top();

            stk.pop();

        }

        if( !stk.empty() ) stk.top()->ch[1] = nw;

        nw->ch[0] = lst;

        stk.push(nw);

    }

    while( !stk.empty() ) {

        root = stk.top();

        stk.pop();

    }

    dfs(root, 0);

    printf("%lld\n", root->ans);

    return 0;

}

@比较正常的题解@

我们实际上是求如图的块的个数。

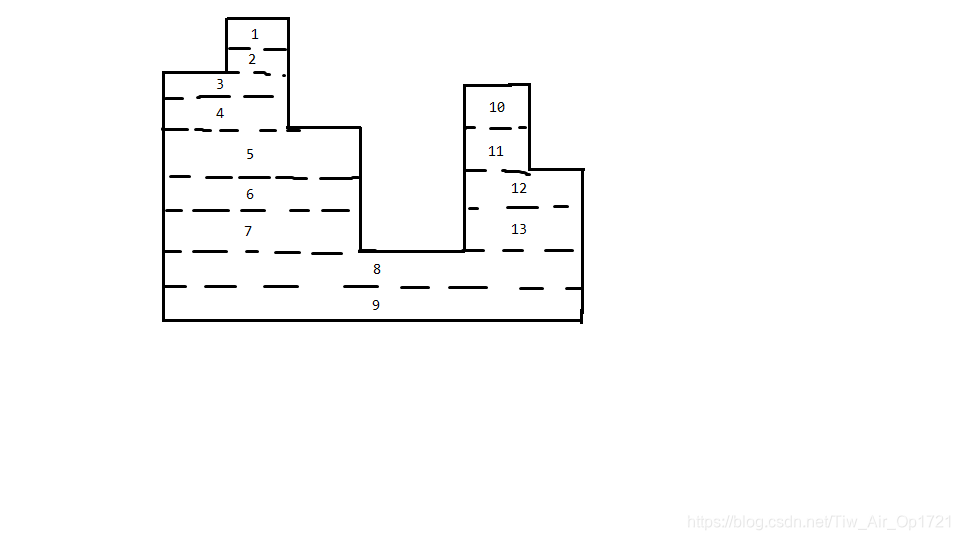
我们不妨在块的右端点去统计每一块对答案的贡献。

所以就很简单了：

（1）如果 d[i] >= d[i+1]，则 ans+=(d[i]-d[i+1])

（2）如果 d[i] < d[i+1]，则 continue

最后 ans+= d[n] 即可

#include<cstdio>

typedef long long ll;

const int MAXN = 100000;

int d[MAXN + 5];

int main() {

    int n; ll ans = 0;

    scanf("%d", &n);

    for(int i=1;i<=n;i++)

        scanf("%d", &d[i]);

    for(int i=1;i<n;i++)

    	if( d[i] >= d[i+1] ) ans += d[i] - d[i+1];

    ans += d[n];

    printf("%lld\n", ans);

}